这是之前朋友出的一道题目，感觉不错，就拿来分享一下。

    问题如下：

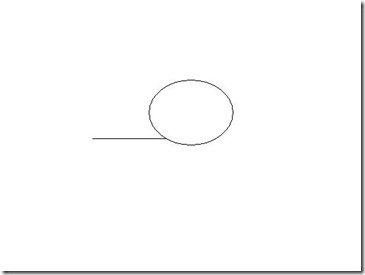
    一个单向链表，怎么判断他是否存在环？

    图示：

    对于最简单的做法就是：

    用一个指针走一圈，如果重复遇到其他任何一个指针，则证明有环。

    但是这样做的问题就是：

    单指针需要留下脚印，会弄脏链表数据，而如果不能脏数据的话，就需要增加一个容器，并且增加查找的开销。

    有没有更好的方法呢？有的，定义一对快慢指针分别为ptr_fast,ptr_slow，ptr_slow走一步，ptr_fast走两步，如果ptr_slow和ptr_fast最终能相遇，那么证明有环。

    解释如下：

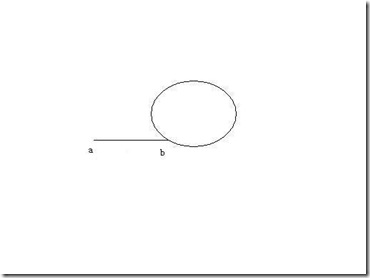
    画图：

    设步长分别为x和y，链表回环结点数为n，非环回环为m

    设经过t次跨步，则只要xt和yt对n同余并且xt和yt都大于m就可以相遇(假设x>y)

    xt-yt=pn

    yt>m

    得到：

    t=pn/(x-y) > m/y(只需pn可整除(x-y))

    指针移动次数为(x+y)t=(x+y)/(x-y)*pn

    而要想pn永远整除(x-y)，那么x-y=1即可。在x-y固定为1的情况下x+y越小，则移动次数越少，也即指针比较次数越少，所以x为2，y为1。

    其实还有第二个问题，即，假设ptr_fast在ptr_slow走完一圈前相遇，那环的长度和链表的长度分别为多少。

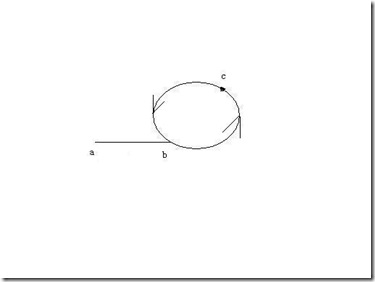
    我们根据第一个问题的结论，假设ptr_fast和ptr_slow在c点相遇。

    图示：

    假设x是速度，t是时间。

    则对ptr_slow:

    ab+bc = x * t

    对ptr_fast:

    ab+bc+cb+bc = 2x*t

    所以得出:

    cb + bc = ab + bc

    即：

    cb = ab

    所以环的长度就求出来了，即bc+cb = bc + ab = ptr_slow走的路程。

    那链表的长度呢？

    现在已经有了ab+bc的长度，只需要知道ab或者cb的长度即可：

    再创建一个指针ptr_new,让ptr_new从head开始，和ptr_slow同时开始走，都是每次一步，由于ab == cb，所以他们相交的地方就是b点。所以即可得到整个链表的长度。

    如果不是在慢指针走一圈内相遇，我还没有想到有算出环的长度和链表长度的方法，大家如果有答案欢迎告知~~

建议继续学习：

1. Linus：利用二级指针删除单向链表    (阅读：11357)
2. Tips of Linux C programming    (阅读：3962)
3. Nginx的connections数组    (阅读：2906)
4. 浅析Linux Kernel中的那些链表    (阅读：2872)