寄存器分配初探–问题描述( Register Allocation – The Problem )
寄存器分配是编译器中一个历久弥新的问题,因为它是编译器在输出汇编代码前必须经历的阶段。寄存器分配算法的好坏,关系着生成代码的性能,大小。为了追求极致性能,很多编译器都在寄存器分配上做了很多文章,不惜引入非常复杂的算法。另一方面寄存器分配算法本身的性能也很关键, 在诸多的JIT编译器(Just-In-Time compiler)中,编译器的性能同时也是程序本身的性能,因此在JIT编译器中还需要关注寄存器分配算法本身的效率问题。
另外,寄存器分配作为将无限多的逻辑单元映射到有限多的物理单元的典型问题,深入了解它也有助于对其他相关问题的理解,如操作系统中的页着色问题(Page Coloring)。这一系列文章将试图对寄存器分配这一问题做些介绍。因为这一问题是编译器中的经典问题,且直到今天都不时有一些研究成果出现,而历史上的相关研究更是浩如烟海,加上博主能力有限,因此只能就其中简单的理论问题做些介绍,试图抛砖引玉,引发更多朋友对该问题的思考。欢迎大家指正、探讨。
这系列文章共四篇:
寄存器分配初探-问题描述
寄存器分配初探-最好的算法:图着色
寄存器分配初探-最快的算法:线性扫描
寄存器分配初探-漫谈
本文是这一系列文章的第一篇,试图说明:为什么要有寄存器分配,这一问题具体是怎样的,并介绍一些相关的专业名词。
1 为什么要有寄存器分配
相信大部分朋友都写过C/C++程序。在这种高级程序设计语言中,程序员可以声明无限多个变量,并为这些变量赋值,对这些变量做运算。每个变量都有自己的作用域,比如在函数内部声明的变量,只在这个函数内部从声明点,到函数返回的范围内都可以访问,操作;全局声明的变量,在整个程序中都有效,程序中的任何一条语句都能访问、操作。
但实际的物理CPU,一般只提供有限多个寄存器用来保存变量。从指令的角度看,计算机程序中的数据都保存在内存中。除了X86结构外,ARM和MIPS基本都采用RISC结构,都需要先将内存中的数据通过访存指令load到寄存器中,再直接在寄存器中做运算。除了个别体系结构的浮点寄存器(X86的浮点寄存器较宽,80bit。此类寄存器只在有浮点数运算的代码中有用。)和向量寄存器(X86的AVX2扩展中,寄存器宽度是256bit,ARM的NEON中,寄存器宽度是128bit。此类寄存器只在向量化代码中有用。)外,X86、ARM、MIPS的整点寄存器都是64位宽。操作这些寄存器的指令可以只操作寄存器中的低32位,或者全部64位。计算机指令将寄存器中的0-1串,按照一定的类型做操作,例如,同样是两个保存在64bit寄存器中的数据,可以使用循环64位右移操作,也可以使用补0的64位右移操作,而他们的运算的结果是不同的。
在编译器看来,对于内建的数据类型,如int,char,指针等类型,因为都是整数,且宽度不大于64bit,因此都能将数据直接保存在寄存器中做运算。对于结构体,字符串等数据大小不确定的,编译器一般都采用基地址(数据结构中第一个域的位置,字符串中第一个元素的位置) + 偏移量的方式,将数据先从内存load到寄存器中操作,再对它们们做运算。 编译器就需要结合整个程序代码,针对代码中的每个语句,确定哪些数据现在应该放到寄存器中,哪些数据需要从内存中取到寄存器,或从寄存器保存到内存中,哪些需要仍需要保持在内存里(对于JIT编译器,只需要对当前需要编译的代码片段)。
如下表所示,为各个存储介质的访问延迟(数据来自《量化》5版。 访问内存和访问寄存器的延迟差别在100~1000倍左右(因为cache由硬件维护,编译器无法控制,我们只考虑最坏情况)。 因为寄存器的数量有限,追求性能的编译器应该为最合适的变量分配寄存器,尽可能的减小程序中的访存操作,进而提升性能。
| 寄存器 | L1 Cache | L2 cache | L3 Cache | 内存 | |
| 访问延迟 | 200ps | 1ns | 3~10ns | 10~20ns | 50~100ns |
| 容量 | 1000B | 64KB | 256KB | 2~4MB | 4~16GB |
以上就是为什么需要寄存器分配算法。
2 为什么寄存器分配很重要
因为寄存器分配算法将会影响到程序中的每一条语句,因此它的好坏,对编译生成的二进制文件的性能非常重要。如果算法设计的不好,将会有更多的访存操作,且访存操作成对出现。 这类访存操作,一般的硬件预测策略很难捕捉,基本都是cache miss的,且都需要写回到内存中。 因此需要长时间占用CPU中的访存功能部件。 虽然不管是MIPS,ARM还是X86,现在都有了精心设计的流水线,乱序发射,但这种访存带来的访存队列阻塞问题还是会非常严重,对性能影响很大。
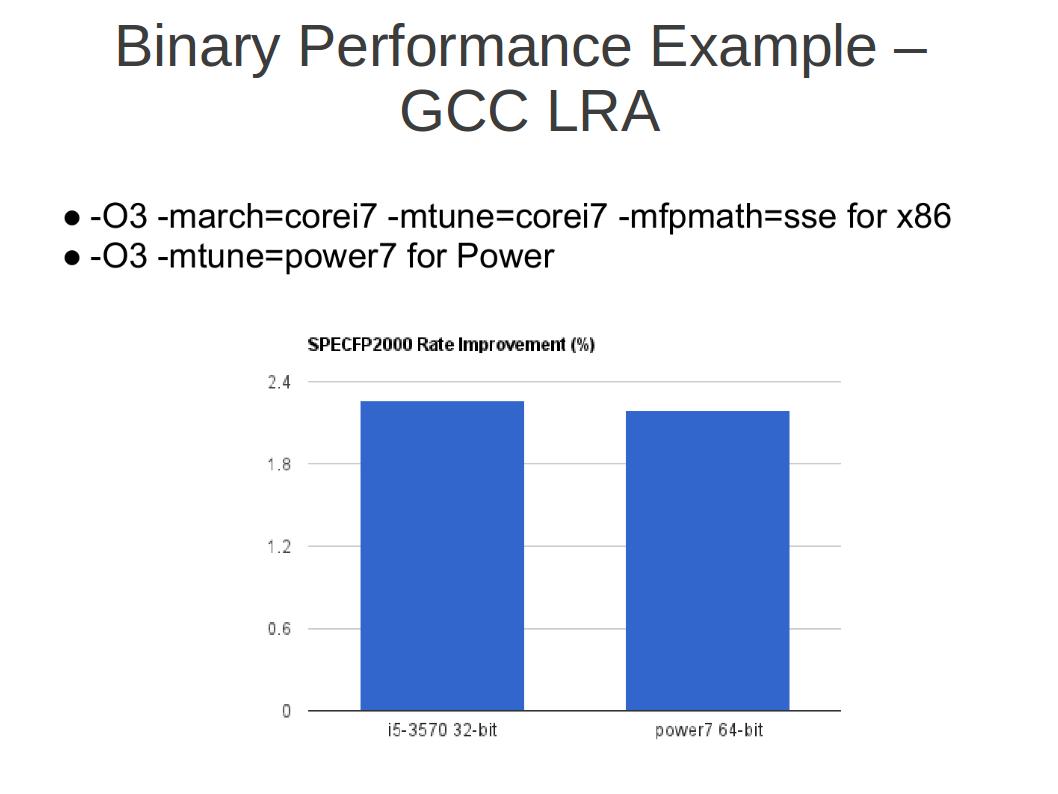
下图是GCC 4.8即将引入的新的LRA寄存器分配算法对性能的提升情况。 GCC中的寄存器分配算法非常复杂(“Only God knows”),已有算法基于现今分配效果最好的图着色算法(在接下来的博文里会详细介绍此算法)。 而新的LRA机制,算是重写了GCC的Reload的阶段,并对局部寄存器分配做了改进(求牛人给出更准确描述)。 可以看到这种改进,在最不规则最权威的桌面通用计算领域性能测试集面前都会有平均2%左右的提升。
图着色算法虽然能很好的解决分配效果问题,但该算法效率太低,算法复杂度高(在下篇博文中会详细解释)。 对于JIT编译,对编译器本身效率要求较高。 因此就需要在分配效果和分配效率之间做一个权衡。 线性扫描算法能很好的满足分配效果和分配效率的权衡关系,因此其改进版本得到了LLVM、Java Hotspot的亲睐(本系列第三篇将详细介绍该算法)。
3 实际编译器中的寄存器分配问题
在实际编译器中,为了尽可能的榨取性能,提升编译器的分配效率,寄存器分配算法都很复杂。 万变不离其宗。不管是GCC,Open64还是LLVM,寄存器分配基本都是在靠近汇编代码输出阶段。 Open64中在寄存器分配之后,几乎没有什么优化了。GCC中,在寄存器分配之后,还存在大约7个PASS(基本块重排序、收集用于调试的变量保存位置相关信息、延迟槽调度、长跳转转换、针对86387浮点寄存器的寄存器到栈变换、汇编代码输出、调试信息输出),也没有优化了。LLVM不清楚,欢迎有了解的朋友补充。
这三个工业界级别的编译器中,到了寄存器分配阶段都已经从语法树形式的中间表示转换成了三地址形式的中间表示。 在GCC中,已经从GIMPLE转换成了RTL;在Open64中,已经从WHIRL转换成了CGIR;在LLVM中,已经从Clang阶段的AST(Abstract Syntax Tree,抽象语法树)转换成了LLVM IR。 在转换成三地址码之前,操作之间的操作数、结果的依赖关系都可以通过树形结构表达,展开成三地址形式之后,就需要大量创建临时变量来表达这种依赖关系。 此时所有的变量(包括临时变量和原程序中的变量),都会被分配伪寄存器(Pseudo Register,伪寄存器和物理寄存器除了数量有区别:无限多个/有限多个外,其他都相同)。
寄存器分配即将这些伪寄存器映射到实际的物理寄存器上 , 因此在寄存器分配之前,要保证指令序列基本不再变化。所以实际编译器中的寄存器分配阶段,基本都在最后阶段,此时都基本完成了几乎所有的底层次优化,如三地址形式的循环优化、指令调度、冗余代码删除、其他窥孔优化等等。但也有例外,比如寄存器分配时,需要额外增加一些访存指令,因此在寄存器分配结束后,可能还需要一些调整。
4 寄存器分配中的一些概念
寄存器分配作为一个历久弥新的话题,在过去的几十年里一直是算法、编译、体系结构、性能优化领域关注的焦点, 因此有了很多专业的概念,来描述其中出现的一些共性问题或共性概念。这里做个简单的介绍,这些概念在一些相似的分配问题中可能也存在,可能名称不同。
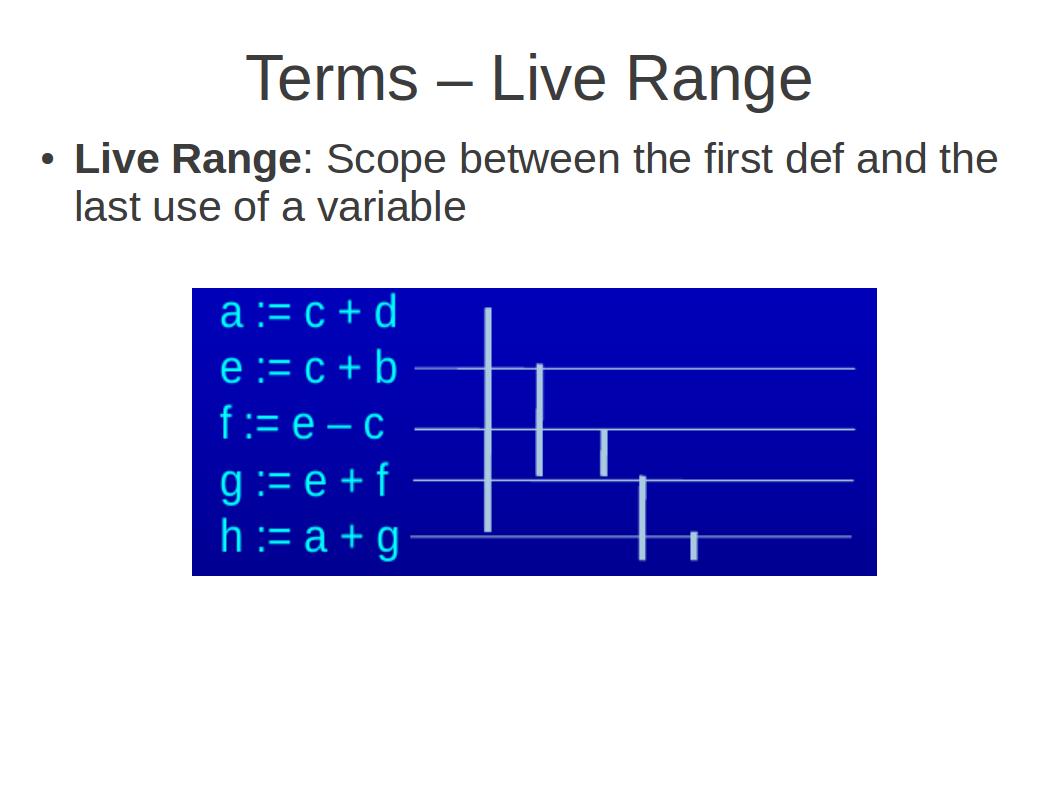
变量的活跃区间(也称生存期,Live Range): 即从变量的第一次定义到最后一次使用之间的范围,即为变量的活跃区间。
干涉(Interference):如果在程序的某个点(即程序运行的某个时刻)P,存在两个变量a和b同时活跃,那么就成为变量a和b在程序运行点P互相干涉。
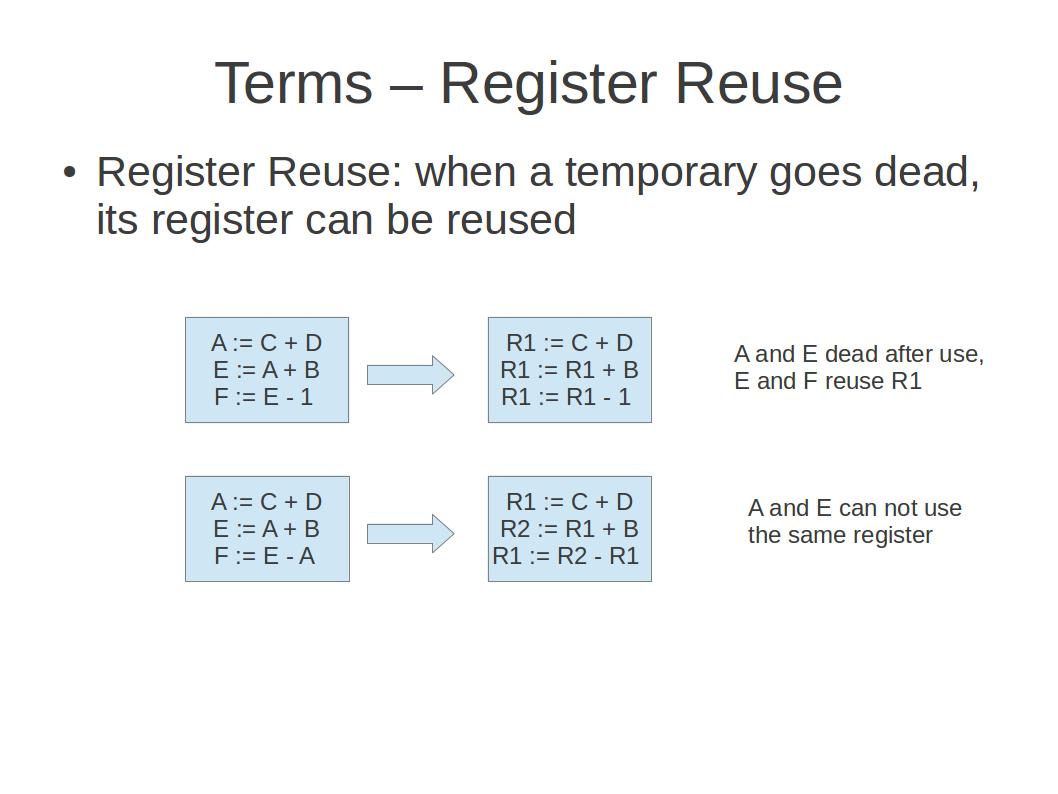
寄存器重用(Register Reuse): 每个变量生命期结束以后,为它所分配的资源(寄存器、内存空间)都可以回收了。将分配给它的寄存器回收,并重新分配给其他变量使用的过程叫做 寄存器重用 。
寄存器压力(Register Pressure): 在程序中的某一时刻,可能会出现需要保存在寄存器中的变量过多,而寄存器不够用的情况,这种情况称为 寄存器压力(Register Pressure)过大 。
寄存器溢出(Register Spilling):当需要映射的逻辑寄存器过多,而物理寄存器较少时,就需要将某些暂时不用的数据挪到内存中,再在需要的时候将其重新搬到寄存器中,这一过程称为 寄存器溢出(Register Spilling).

以上这些概念,都是我们将在接下来探讨寄存器分配的过程中经常遇到的概念,这里先来个简单的介绍。
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:erlv 来源: 编译点滴
- 标签: 寄存器
- 发布时间:2012-12-11 13:37:27
-
 [927] WordPress插件开发 -- 在插件使用
[927] WordPress插件开发 -- 在插件使用 -
 [126] 解决 nginx 反向代理网页首尾出现神秘字
[126] 解决 nginx 反向代理网页首尾出现神秘字 -
 [51] 如何保证一个程序在单台服务器上只有唯一实例(
[51] 如何保证一个程序在单台服务器上只有唯一实例( -
 [50] 整理了一份招PHP高级工程师的面试题
[50] 整理了一份招PHP高级工程师的面试题 -
 [48] CloudSMS:免费匿名的云短信
[48] CloudSMS:免费匿名的云短信 -
 [48] Innodb分表太多或者表分区太多,会导致内
[48] Innodb分表太多或者表分区太多,会导致内 -
 [48] 用 Jquery 模拟 select
[48] 用 Jquery 模拟 select -
 [48] 全站换域名时利用nginx和javascri
[48] 全站换域名时利用nginx和javascri -
 [48] 海量小文件存储
[48] 海量小文件存储 -
 [46] ps 命令常见用法
[46] ps 命令常见用法