为什么算法渐进复杂度中对数的底数总为2
浏览:3109次 出处信息
在分析各种算法时,经常看到
三分式归并排序的时间复杂度
先看一个小例子。
大多数人应该对归并排序(merge sort)很熟悉,它的渐进复杂度为
递归分析
下面通过递归分析对三分式归并排序的时间复杂度进行分析。因为不管是三分还是二分,对于总共n个数据来说,一遍合并的复杂度为
如果把这个递归式的递归树画出来,很容易得到
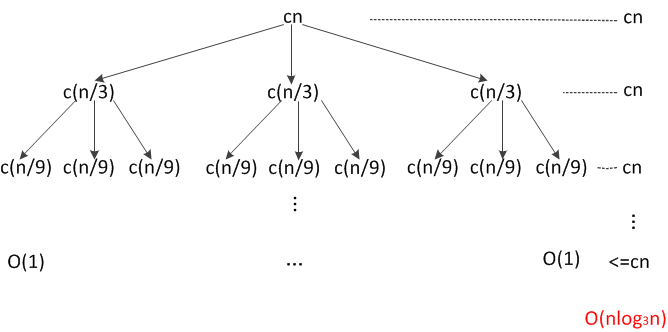
对数的陷阱
那么这是否意味着三分式归并排序在时间复杂度上要优于二分式的归并排序呢?因为直觉上
实际上三分式归并排序的时间复杂度确实是
这看起来似乎是矛盾的,
其中a和c均大于0且不等于1。
更多内容详见原文:http://blog.codinglabs.org/articles/why-logarithm-base-of-asymptotic-time-complexity-always-two.html
QQ技术交流群:445447336,欢迎加入!
扫一扫订阅我的微信号:IT技术博客大学习
扫一扫订阅我的微信号:IT技术博客大学习
<< 前一篇:内存异常排查
后一篇:开源压缩算法Zopfli介绍 >>
文章信息
- 作者:CodingLabs 来源: CodingLabs
- 标签: 渐进复杂度
- 发布时间:2013-03-03 23:10:09
近3天十大热文
-
 [917] WordPress插件开发 -- 在插件使用
[917] WordPress插件开发 -- 在插件使用 -
 [135] 解决 nginx 反向代理网页首尾出现神秘字
[135] 解决 nginx 反向代理网页首尾出现神秘字 -
 [54] 整理了一份招PHP高级工程师的面试题
[54] 整理了一份招PHP高级工程师的面试题 -
 [53] 如何保证一个程序在单台服务器上只有唯一实例(
[53] 如何保证一个程序在单台服务器上只有唯一实例( -
 [52] Innodb分表太多或者表分区太多,会导致内
[52] Innodb分表太多或者表分区太多,会导致内 -
 [52] 海量小文件存储
[52] 海量小文件存储 -
 [51] 全站换域名时利用nginx和javascri
[51] 全站换域名时利用nginx和javascri -
 [51] 用 Jquery 模拟 select
[51] 用 Jquery 模拟 select -
 [50] CloudSMS:免费匿名的云短信
[50] CloudSMS:免费匿名的云短信 -
 [48] jQuery性能优化指南
[48] jQuery性能优化指南