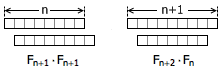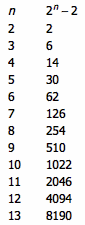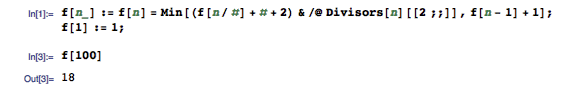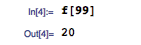你或许熟知一个非常经典的结论： Fibonacci 数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … （头两项都是 1 ，此后每一项都是前两项之和）的相邻两项之比将会越来越接近黄金比例 0.618 。。。。

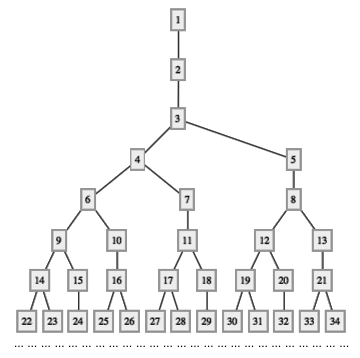
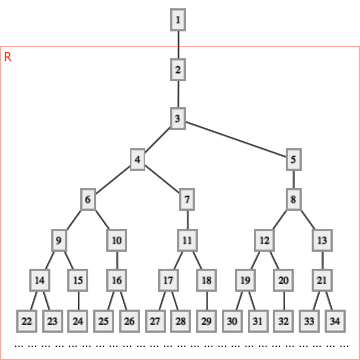
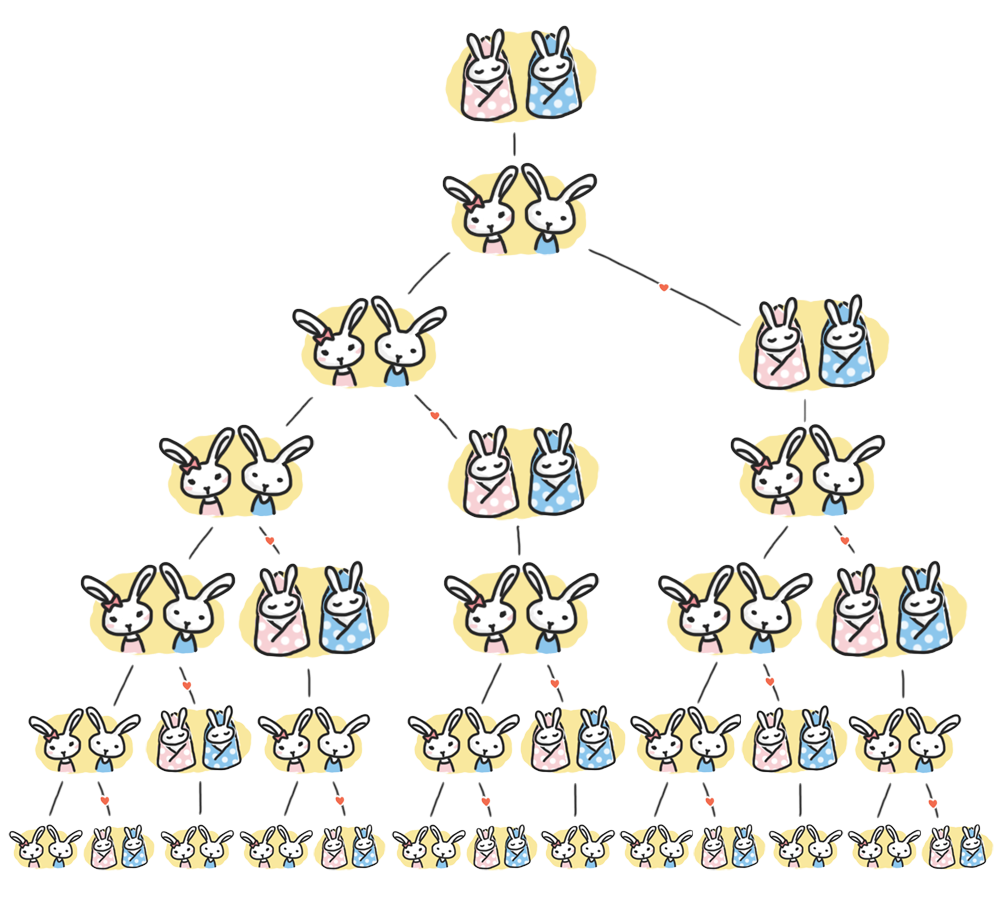
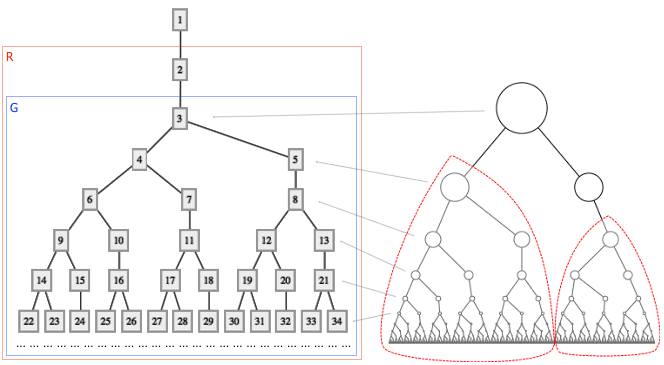
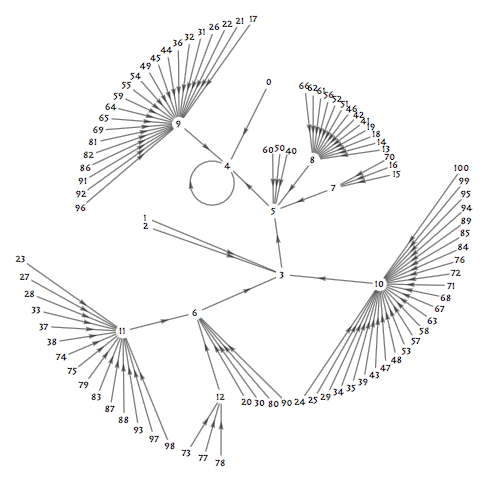
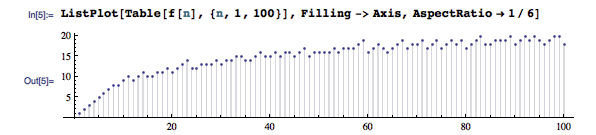
    在著名奇书 Gödel, Escher, Bach: An Eternal Golden Braid 的第五章中，为了展现出递推序列的神奇之处，作者 Douglas Hofstadter 定义了这么一个递推序列： G(n) = n - G(G(n - 1)) ，其中 G(1) = 1 。这个数列通常被称作 Hofstadter G-sequence 。它有什么特别的地方呢？

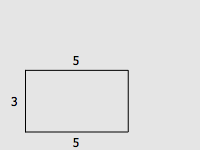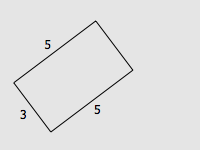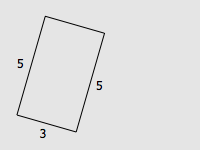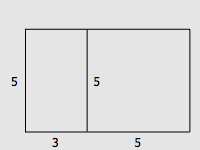
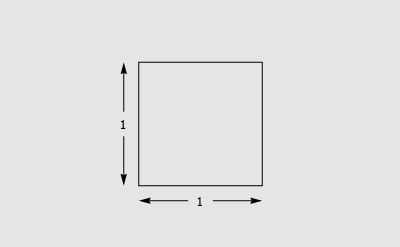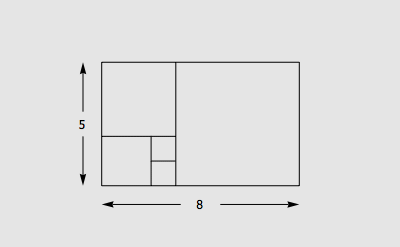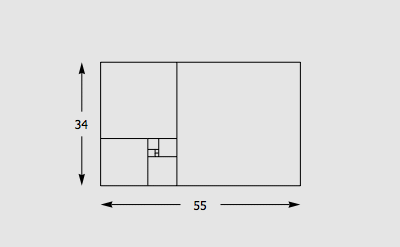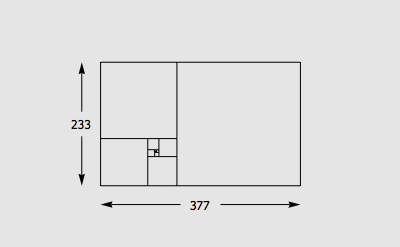
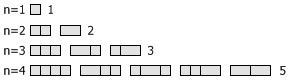
        数列 1, 1, 2, 3, 5, 8, 13, 21, 34, … 叫做 Fibonacci 数列。这个数列有很多神奇的性质，其中一个性质是，每一个 Fibonacci 数的平方与它前后两个 Fibonacci 数的乘积相比一定正好相差 1 。具体地说，如果把第 n 个 Fibonacci 数记做 Fn ，那么有：       Fn+1 · Fn+1 - Fn · Fn+2 = (-1)n     今天看到了这个定理的一个组合数学证明，觉得非常有意思，在这里和大家分享。     Fibonacci 数有很多组合数学上的意义。比如说，用 1 × 1 和 1 × 2 的积木覆盖一个 1 × n 的棋盘，总

        这道题的答案有几个字母？答案：four。     有趣的是，这是唯一的答案。如果令函数 f(n) 表示正整数 n 的英文表达中有多少个字母， n=4 是该函数的唯一不动点。  

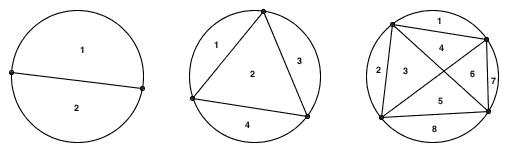
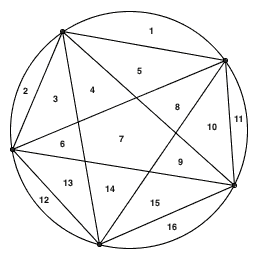
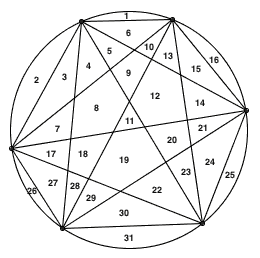
        数学猜想并不总是对的，错误的数学猜想不占少数。只不过因为反例太大，找出反例实在是太困难了。这篇日志收集了很多“大反例”的例子，里面提到的规律看上去非常诱人，要试到相当大的数时才会出现第一个反例。千万不要迷信规律     圆上有 n 个点，两两之间连线后，最多可以把整个圆分成多少块？            上图显示的就是 n 分...

        最近在做网站测试时，遇到了需要在输入框输入 3000 字的测试用例。联想到平时聊天时经常复制粘贴一堆笑脸刷屏讨 MM 欢心的行为，不由想到了一个有趣的问题：为了输入一定数量的字符，最少需要按多少个键？     大家最常用的策略或许是， 先输一些字符，然后全选复制，粘贴到一定规模后，再全选复制，粘贴到一个新的数量级，如此反复。注意到进入全选状态（并且复制后），第一次粘贴将...