专题：数学 -- IT技术博客大学习 -- 共学习共进步！

[Java基础教程]第六章-Java数学运算符

最初设计计算机的目的是为二战中的盟国军队计算导弹的轨迹，数学计算是计算机的最初目的，本章我们共同学习一下最基础的数学四则运算符。

数学之美：Marden定理

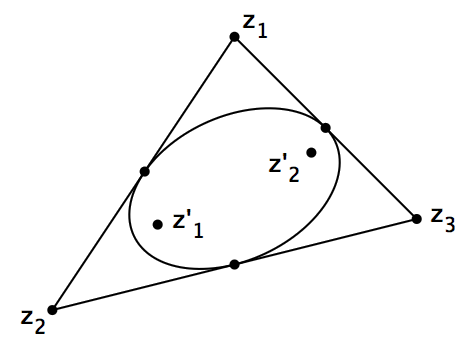
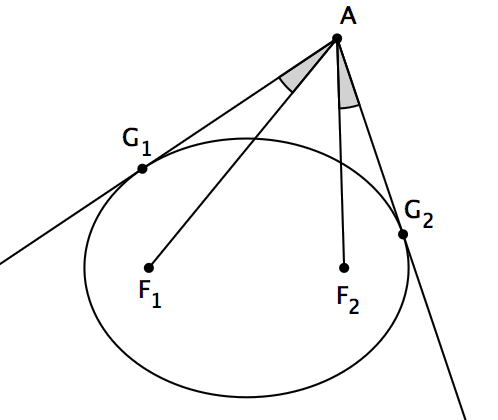
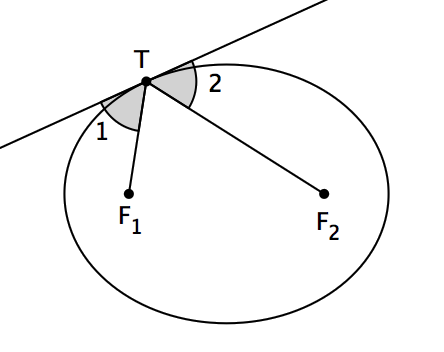
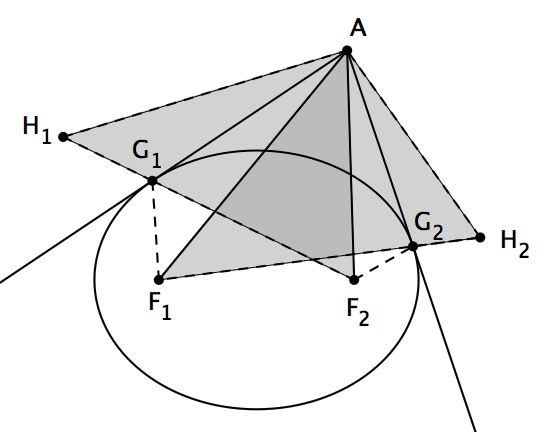
设 p(z) 是一个复数域上的三次多项式， z1 、 z2 、 z3 是 p(z) 的三个根，它们在复平面上不共线。那么，在这个复平面上存在唯一的椭圆，使得它与三角形 z1z2z3 的各边都相切，并且都切于各边的中点处。并且，这个椭圆的两个焦点是 p'(z) 的两根。

难倒犹太人的11个数学问题

这个并不是标题党。很多年以前，要想进入莫斯科国立大学的数学系，你必须通过四项入学考试；头两个都是数学考试，一个笔试，一个面试。在面试中，学生和考官都是一对一的，考官可以自由向学生提出任何他喜欢的问题。考官们都准备了很多“棺材问题”，这些问题的答案非常简单，但由于思路太巧妙了，以至于学生很难想到。考官便可以以“你连这个都没想到”为理由，光明正大地拒绝学校不想要的人（主要是犹太...

千万别学数学：最折磨人的数学未解之谜（二）

数学之美不但体现在漂亮的结论和精妙的证明上，那些尚未解决的数学问题也有让人神魂颠倒的魅力。和 Goldbach 猜想、 Riemann 假设不同，有些悬而未解的问题趣味性很强，“数学性”非常弱，乍看上去并没有触及深刻的数学理论，似乎是一道可以被瞬间秒杀的数学趣题，让数学爱好者们“不找到一个巧解就不爽”；但令人称奇的是，它们的困难程度却不亚于那些著名的数学猜想，这或许比各个领域中艰深的数学难题...

数学常数e的含义

e是一个重要的常数，但是我一直不知道，它的真正含义是什么。...

集数学与艺术于一体的几何幻方

Lee Sallows 最近做了一个网站，收集了很多在几何意义上也成立的幻方，集数学与艺术于一体，为传统意义的幻方赋予了新的生命。大家来欣赏一下吧。这是一个幻方，它由九块积木组成。这些积木所含的小方格数恰好是从 2 到 18 的偶数，每行每列和两对角线上的方格总数都是 30 。牛 B 的是，每条线上的三块积木正好也都能拼成一个 6 × 5 的矩形。与上图类似的一个几何幻方，不过明显更帅一些。

看来看去都是看数学书

计算机需要数学，这是无庸置疑的。可是有些事情还是很 shocking. 比如，全世界的程序员都写函数式编程写得好好的，用着只要小学生就理解的 LOGO 升级版

从一道题目谈计算机和数学

统计从1至400亿之间的自然数中含有多少个1？比如1-11中，有1，10，11这三个自然数有4个1。拿到这道题目，您会如何去计算呢？如果是计算机方面的面试，你又该如何去思考呢？也有同事拿这道题目谈到了“数学”与“数感”的理解，不过笔者却想谈一些更实际一些东西。如果是计算机方面的出现这道题目，我们可能首先想到的是挨个去找。比如1含有一个1,然后2不含有1，…10含有1个1, 11含有2个1，….直到4亿。实际...