先简单说一下公钥密钥的非对称算法的概念，平常我们用的加密算法往往都是对称的，也就是说加密密钥和解密密钥是一样的，比如凯撒密码，你把每个字母后移3位，a变成d，b变成e，这里3就是加密密钥，然后解密的时候前移3位，这时候3就是解密密钥，非对称加密顾名思义就是加密密钥和解密密钥是不同的，恩，数学就是能干很多神奇的事情啊。

    数论，数学中的皇冠，最纯粹的数学。早在古希腊时代，人们就开始痴迷地研究数字，沉浸于这个几乎没有任何实用价值的思维游戏中。直到计算机诞生之后，几千年来的数论研究成果突然有了实际的应用，这个过程可以说是最为激动人心的数学话题之一。

    从同事那里借来了一本单墫教授主编的《初等数论》奥数书，看到很多精彩的问题，在这里做个笔记，与大家一同分享。不少问题和答案都有过重新叙述，个别问题有所改动。   问题：找出所有使得 2n - 1 能被 7 整除的正整数 n 。答案：由于 2n 的二进制表达为 1000…00 （n 个 0），因此 2n - 1 的二进制表达为 111…11 （n 个 1）。而 7 的二进制表达是 111 ，要想让它整除 n 个 1 ，显然 n 必须是也只能是 3 的倍数。 问题：是否存在 100 个数，使得它们的和等于它们的最小公倍数？答案...

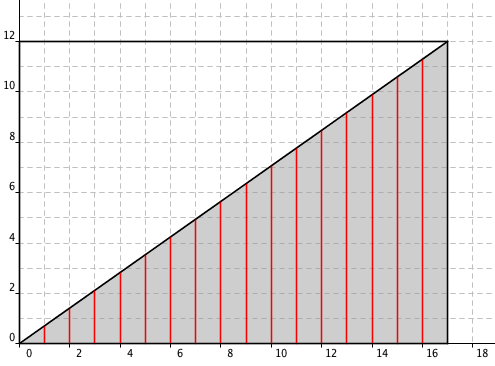
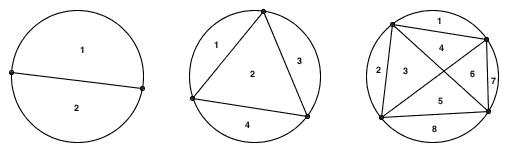
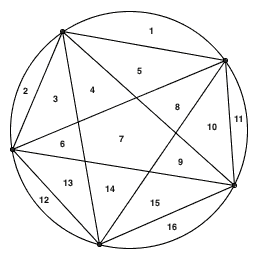
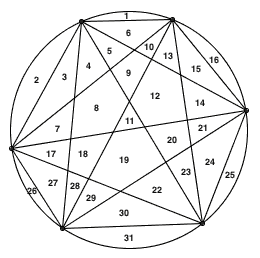
        数学猜想并不总是对的，错误的数学猜想不占少数。只不过因为反例太大，找出反例实在是太困难了。这篇日志收集了很多“大反例”的例子，里面提到的规律看上去非常诱人，要试到相当大的数时才会出现第一个反例。千万不要迷信规律     圆上有 n 个点，两两之间连线后，最多可以把整个圆分成多少块？            上图显示的就是 n 分...