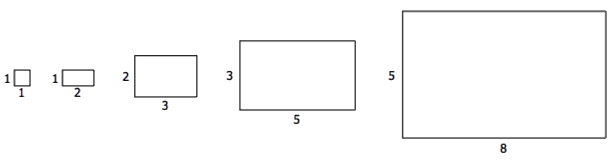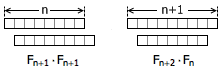您现在的位置:首页 --> 查看专题: Fibonacci
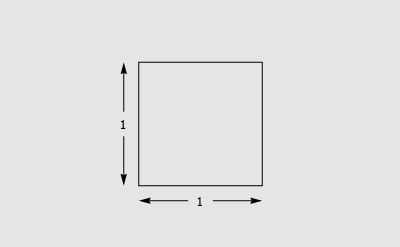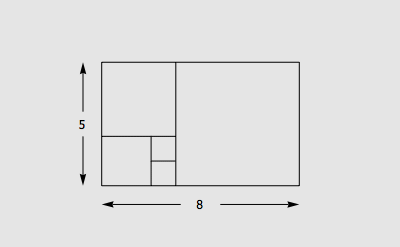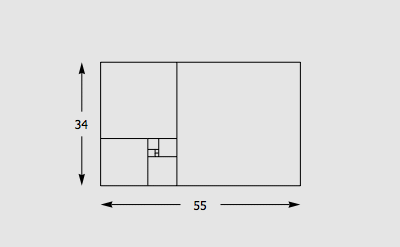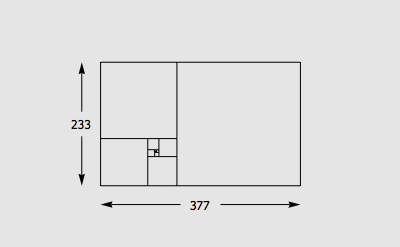
你或许熟知一个非常经典的结论: Fibonacci 数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … (头两项都是 1 ,此后每一项都是前两项之和)的相邻两项之比将会越来越接近黄金比例 0.618 。。。。
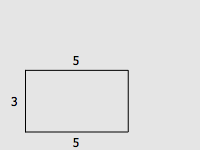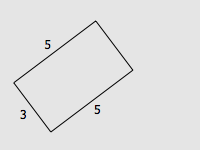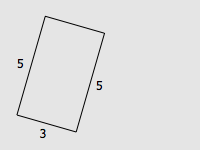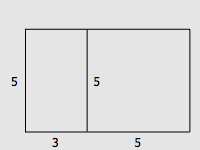
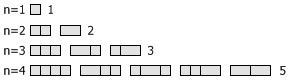
数列 1, 1, 2, 3, 5, 8, 13, 21, 34, … 叫做 Fibonacci 数列。这个数列有很多神奇的性质,其中一个性质是,每一个 Fibonacci 数的平方与它前后两个 Fibonacci 数的乘积相比一定正好相差 1 。具体地说,如果把第 n 个 Fibonacci 数记做 Fn ,那么有: Fn+1 · Fn+1 - Fn · Fn+2 = (-1)n 今天看到了这个定理的一个组合数学证明,觉得非常有意思,在这里和大家分享。 Fibonacci 数有很多组合数学上的意义。比如说,用 1 × 1 和 1 × 2 的积木覆盖一个 1 × n 的棋盘,总
[ 共2篇文章 ][ 第1页/共1页 ][ 1 ]
近3天十大热文
-
 [1152] WordPress插件开发 -- 在插件使用
[1152] WordPress插件开发 -- 在插件使用 -
 [60] 解决 nginx 反向代理网页首尾出现神秘字
[60] 解决 nginx 反向代理网页首尾出现神秘字 -
 [51] Java开发岗位面试题归类汇总
[51] Java开发岗位面试题归类汇总 -
 [44] web开发设计人员不可不用的在线web工具和
[44] web开发设计人员不可不用的在线web工具和 -
 [33] Rax 系列教程(长列表)
[33] Rax 系列教程(长列表) -
 [33] 手机产品设计方向
[33] 手机产品设计方向 -
 [32] 一句话crontab实现防ssh暴力破解
[32] 一句话crontab实现防ssh暴力破解 -
 [30] 如何建立合适的索引?
[30] 如何建立合适的索引? -
 [28] oracle技术方面的路线
[28] oracle技术方面的路线 -
 [28] 程序员疫苗:代码注入
[28] 程序员疫苗:代码注入
赞助商广告