从混乱到秩序――关于比例与构成的设计探讨





在很多艺术品以及大自然中都能找到它。
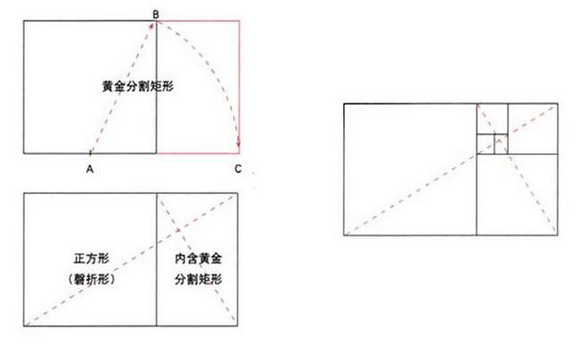
由上图可以简单理解黄金分割矩形的形成:
1.一个正方形边线的中点A向对角B画一条斜线,以斜线为半径画出的弧线,与正方形的延长线相交于C点。构成一个黄金矩形;
2.大矩形和小矩形的对角线和边线的相交点,成为黄金二次分割的起始线;
3.这个分割过程可以无限继续下去,产生许多更小的等比的矩形和正方形。

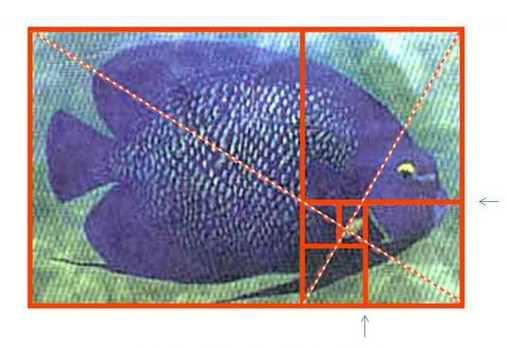
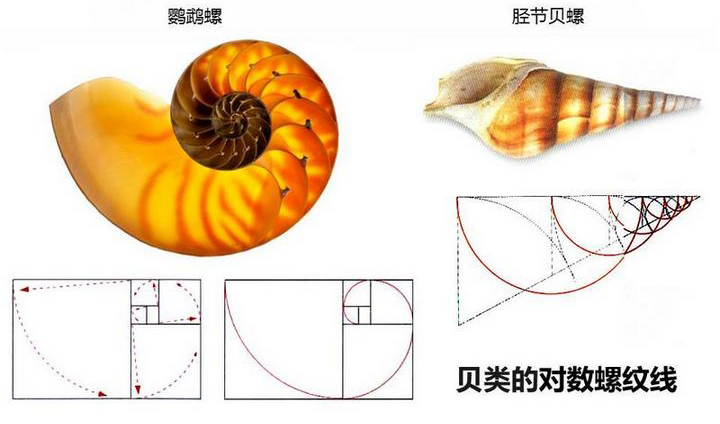
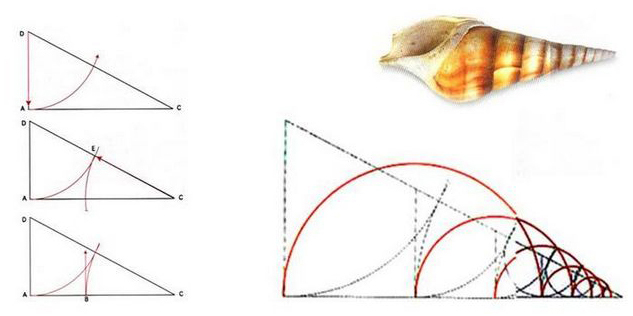
从胫节贝螺的生长螺纹线可以看出:
黄金分割三角形是它不断趋向完美生长的方式,每一个节点都是一个轮回的起点,这样神秘的几何学生长规律,已经成为许多科学研究与艺术研究的课题。
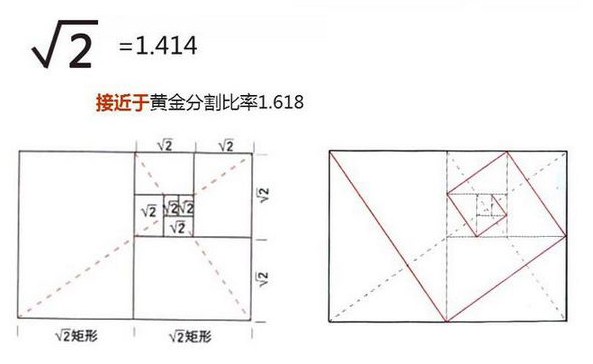
√2矩形具有特殊的性质,能被无限分割为 等比 更小的矩形。
√2矩形,具有特殊的性质:
它能被无限分割为等比、更小的矩形。它接近于黄金分割比例的1.618,
√2矩形比例是欧洲DIN纸张尺寸体系的基础,这个标准体系不仅简单快捷,它的特殊规律性,在最大限度利用纸张没有任何浪费。
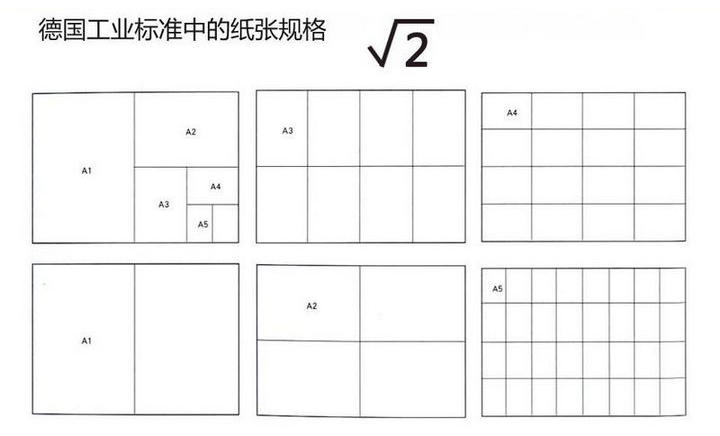
这是我们身边打印室中常见的纸张规格,其实一些看似不相关的数值或比例,都是有规律可寻的,需要我们进一步去认识它们和学会使用它们。
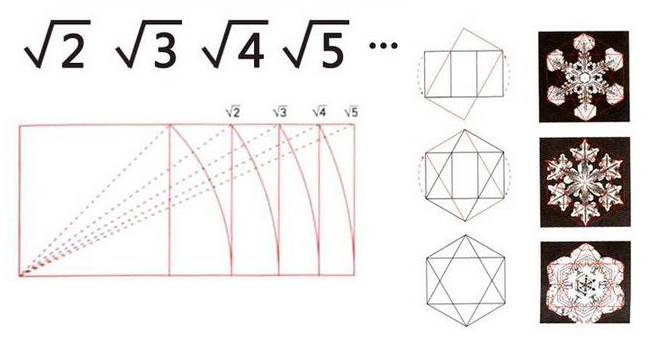
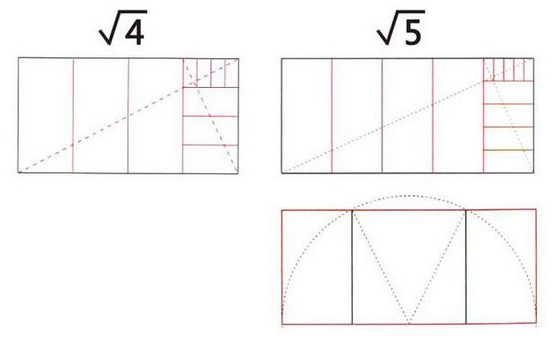
√3,√4,√5矩形之间的规律,我们可以由上图看出:
√3矩形是由√2矩形的对角线,作为半径画出的弧线相交点的垂直延长线所构成,同理√4,√5也是这样推导,
√3矩形具有构成一个正六棱柱结构的特性,能在雪花晶体的形状、蜂巢和自然界许多地方找到。
在后面的举例中,我们也能找到这些完美黄金分隔几何图形的影子。

比萨的列奥纳多,又称斐波那契(Leonardo Pisano ,Fibonacci, Leonardo Bigollo,1175年-1250年),意大利数学家,西方第一个研究斐波那契数,并将现代书写数和乘数的位值表示法系统引入欧洲。

斐波那契数列还有两个有趣的性质:
1.斐波那契数列中任一项的平方数都等于跟它相邻的前后两项的乘积加1或减1;
2.任取相邻的四个斐波那契数,中间两数之积(内积)与两边两数之积(外积)相差1
用这个数列解释兔子繁衍问题,是个比较有趣的过程:感兴趣的童鞋可以详细解一下:http://baike.baidu.com/view/112871.htm
接下来我们可以欣赏一下古希腊雕塑中的人体比例规律:
人体和许多动植物一样,也具有黄金分割率,多里夺弗罗斯和宙斯,它们两个人的比例几乎一样

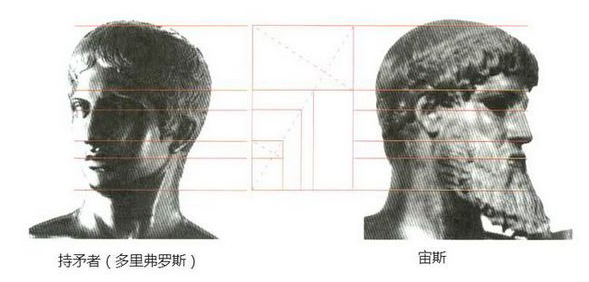
用一个黄金分割矩形来分析头部的高和宽。
这个黄金分割矩形又被更小的黄金分割矩形进一步划分,以控制面部器官的位置。
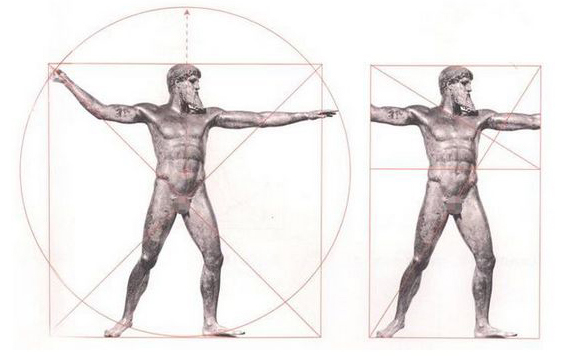
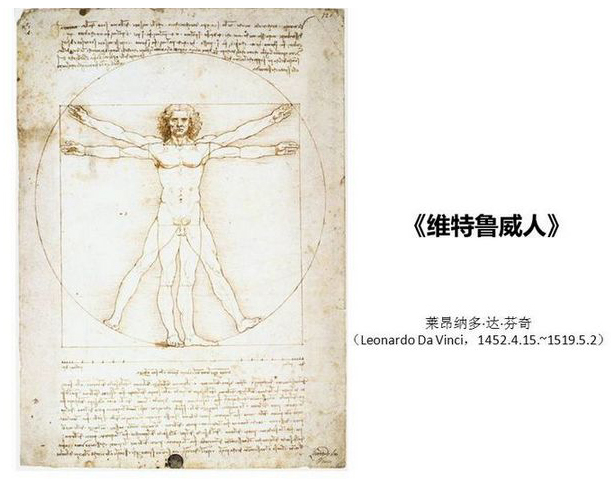
这是一幅达・芬奇依照维特鲁威定律所作的钢笔画素描,现藏于威尼斯的学院美术馆。
这幅素描中所画的男子形象被世界公认为是最完美的人体黄金比例。

并且首次谈到了把人体的自然比例应用到建筑的丈量上,总结出了人体结构的比例规律。
达・芬奇的《蒙娜丽莎》《最后的晚餐》等美术巨作同样也运用维特鲁威原理。
正面复合多重黄金分割矩形,二次黄金分隔矩形构成楣梁、中楣和山形墙的高。

巴黎圣母院大教堂 黄金分隔矩形中的正方形围住了在大教堂正面主体部分,二次黄金分隔围住了两座塔楼。


从中可以明白那些几何构成方法的是直觉地?深思熟虑地?还是偶然的?


朱尔.谢雷,这张捕捉舞蹈演员动作而设计的迷人生动海报,初看这些元素的构成都是随机的,但通过几何学构成分析,我们可以看到画面的构成是由圆形、五边形、五角星,以及黄金三角构成,画面中心的女性臀部正好落在圆心上。
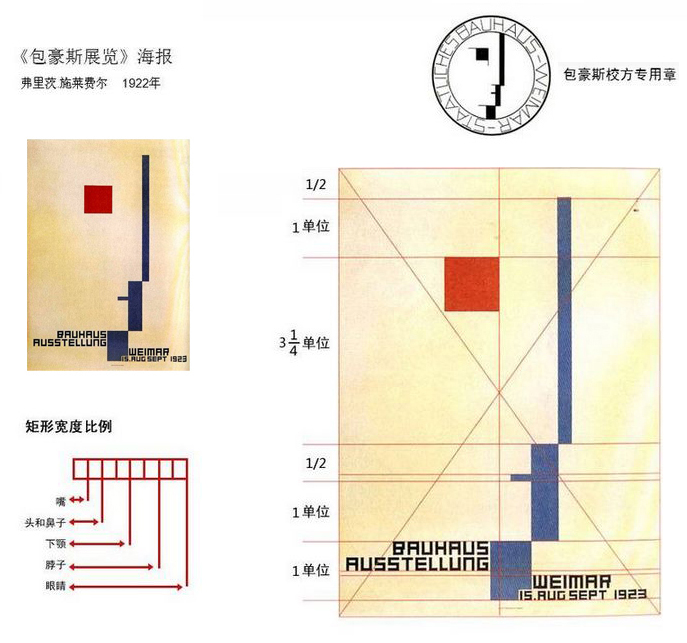


水天相接的水平线将海报一分为二,橙色遮阳伞的较小的椭圆轴通过海报的中心,起到平衡构图的作用;
两人物分别位于这个轴的左右,在色彩和形状上也提供了一种平衡。



在近代海报和设计构图原理中,也能见到黄金分割原理的影子,人们善用它来讲比例合理划分,让画面趋向完美。

很难相信70多年前就能设计和生产出这样一件具有现代感的经典家具;椅子的侧视图和前视图,正好是正方形,靠椅的花纹块状近似为一些小的根号2矩形;
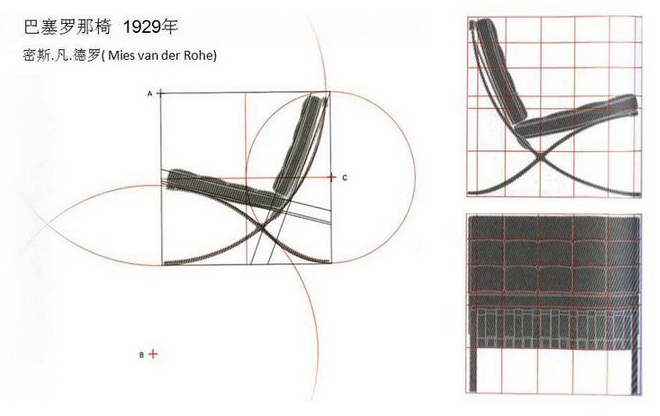

侧窗重复了黄金分割椭圆的形状,车门在一个正方形内,复合黄金分割矩形;
车外观各细节变化部分都与黄金分割和正圆相切;
现在,有新的灵感来运用这些技术在我们自己的作品中创造对称、有序和视觉平衡美了么?
呵呵……
文参考献:
《Geometry of Design:Studies in Proportion and Composition 》(设计几何学)作者:Kimberly Elam 译者: 李乐山
《Universal Principles of Design 》作者: 威廉
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:CDCer 来源: 腾讯CDC
- 标签: 构成 比例 混乱 秩序
- 发布时间:2010-12-21 01:53:59
-
 [1197] WordPress插件开发 -- 在插件使用
[1197] WordPress插件开发 -- 在插件使用 -
 [90] 解决 nginx 反向代理网页首尾出现神秘字
[90] 解决 nginx 反向代理网页首尾出现神秘字 -
 [43] web开发设计人员不可不用的在线web工具和
[43] web开发设计人员不可不用的在线web工具和 -
 [30] Rax 系列教程(长列表)
[30] Rax 系列教程(长列表) -
 [29] 手机产品设计方向
[29] 手机产品设计方向 -
 [29] 如何建立合适的索引?
[29] 如何建立合适的索引? -
 [28] 一句话crontab实现防ssh暴力破解
[28] 一句话crontab实现防ssh暴力破解 -
 [28] Java开发岗位面试题归类汇总
[28] Java开发岗位面试题归类汇总 -
 [26] 程序员疫苗:代码注入
[26] 程序员疫苗:代码注入 -
 [25] 我对学习oracle与成长的理解
[25] 我对学习oracle与成长的理解