最近忙于写学年论文，一直没时间更新 Blog 。不过，我却并没有停止在网上闲逛的习惯。这几天会慢慢把最近看到的有意思的东西写下来。今天学到的一个比较有趣的东西就是：平均等待时间往往大于平均间隔时间的一半。

     比方说，有这么一趟公交车，平均每 10 分钟发一班车，但具体的发车时间是很不固定的。如果你在某个时刻来到车站，等到下一班车平均要花多久呢？很多人或许都觉得，平均等待时间应该是 5 分钟，毕竟平均间隔时间是 10 分钟嘛。然而事实上，平均等待时间是大于 5 分钟的。这是因为，10 分钟的发车间隔只是一个平均值，实际间隔有时是几分钟，有时是十几分钟。如果你出现在车站的时刻，正好位于几分钟的间隔中，你的平均等待时间显然就会小于 5 分钟；但如果你出现在车站的时刻，正好位于较长的间隔中，那么你的平均等待时间就会大于 5 分钟。关键就在这里：你出现在车站的时刻，更有可能落在了较长的发车间隔中。因而，平均等待时间会偏向于大于 5 分钟的情况。

     那么，如果公交车发车的时间足够随机，概率均等地分布在时间轴上(假设平均间隔仍是 10 分钟)，那么当你来到车站时，平均需要多久才能等到公交车呢？答案或许很出人意料――平均等待时间就是 10 分钟。下面我们就来证明这一点。

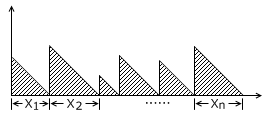
     首先注意到，如果发车间隔依次为 X1, X2, …, Xn ，出现在车站的时刻不同，等候时间也会不同，其函数图象大致是锯齿形的。而平均等待时间，就是这个函数图象的平均高度，或者说所有阴影部分的面积和(也就是 X1, X2, …, Xn 的平方和的一半)除以这段时间总长(也就是 X1, X2, …, Xn 的和)。如果用 W 来表示平均等待时间的话，则

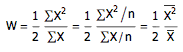
     另外，由于公交车的发车时间是完全随机的，因而发车间隔长度服从指数分布 λe-λx ，它的平均值 μ = 1/λ ，方差 σ2 = 1/λ2 ，后者正好是前者的平方。如果把上述所有 X 的方差记作 Var(X)，那么

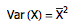
     但是

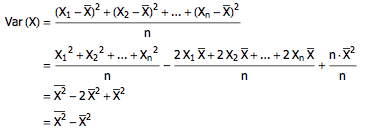
     因此

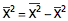
     也就是

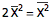
     所以说

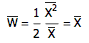
     这就表明，平均等待时间就是平均间隔时间！

     当然，转念一想，你会发现这其实并不难理解。由于发车时间是完全随机的，过去的都已经过去了，并不会对未来造成影响。也就是说，当你开始等车时，知道前面那趟车已经走了很久了，并不意味着下一班车就会更快到来。不管你出现在时间轴的什么位置，等到下一班车的平均时间都是一样的――平均的间隔时间。

     参考资料：

     http://mahalanobis.twoday.net/stories/3486587/

建议继续学习：

1. 查询Linux系统最后重启时间的三个方法    (阅读：3492)
2. Shell Tips: Unix 时间到字面    (阅读：2628)
3. 时间time_t和string(char*)格式互转    (阅读：2569)
4. Linux下如何查看系统启动时间和运行时间    (阅读：2552)
5. php获取文件创建时间、修改时间    (阅读：2447)
6. linux时间相关结构体和函数整理    (阅读：2450)
7. linux 查看自己系统装于何时    (阅读：2412)
8. python中对时间处理的几个函数    (阅读：2383)
9. 如何正确地处理时间    (阅读：2191)
10. 在 Perl 下处理时间的小技巧 strftime    (阅读：2062)