趣题:所有人手上的糖数最终会变得一样多
n 个小朋友在圆桌上坐成一圈。初始时,每个小朋友都拥有一定数量的糖。接下来,反复进行下面两个操作:
1. 如果有人手里的糖数是奇数,就向老师再要一颗糖,把手里的糖数补成偶数;
2. 每个人都把自己手中一半的糖传给他右边的人(同时接到从左边传过来的糖)。
证明:总有一个时刻,所有小朋友手中都会拥有相同数量的糖。
附加题:这是一个非常经典的问题。猜猜看我最早在什么地方看到的这个问题?
我很小很小的时候,就在《十万个为什么》的数学分册 1 上读到了这个问题。在我看过的所有书里,这本书恐怕是历史最悠久,被我翻得最烂,对我意义最大的书了。我甚至还记得书里那篇文章的标题――《怎样调整,使大家的糖一样多》。不过,让人哭笑不得的是,文章中用大量篇幅演示了结论的意思,最终却并没有给出一个证明。于是,究竟该怎样证明这个结论,便成了一桩“悬案”。今天在这里看到这个问题的证明时,实在是有些激动,毫不犹豫地把它记了下来。
在第一次传糖之前,每个人手里的糖数都会被补成偶数。因此,我们可以直接假设初始时所有人手里的糖数都是偶数。把所有人手中的糖数的最大值记作 M 。下面,让我们考虑任意一个小朋友,假设他手中的糖数为 a ,他左边的人手中的糖数为 a\' 。第一次传糖之后,这个人手里的糖数就变成了 (a + a\') / 2 。由于 a 和 a\' 都不超过 M ,因而要么 (a + a\') / 2 正好等于 M (但由于 M 是偶数,因此他不能再向老师要糖了),要么 (a + a\') / 2 将会严格小于 M (即使之后再向老师要一颗糖,最多也只能刚好达到 M )。因此,在第二次传糖之前,每个人手中的糖数仍然都不超过 M 。由此可见,不断继续下去,今后任何人在任何时刻手中的糖数都不会超过 M 。
这表明,所有人的糖数之和有一个上限。因此,小朋友们手中的总糖数不会无限制地增加,总有一个时候,所有人都不再得到新的糖了,整个过程只剩下 n 个数值间简单的迭代。接下来,神奇的一步出现了。让我们考虑在此之后,每一次传糖将导致所有人的糖数的平方和会如何变化:
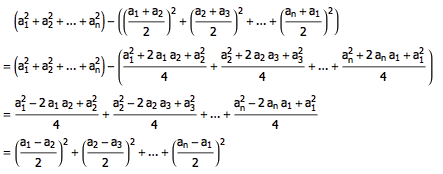
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:Matrix67 来源: Matrix67: My Blog
- 标签: 糖
- 发布时间:2011-11-16 23:41:00
-
 [1120] WordPress插件开发 -- 在插件使用
[1120] WordPress插件开发 -- 在插件使用 -
 [55] Java开发岗位面试题归类汇总
[55] Java开发岗位面试题归类汇总 -
 [52] 解决 nginx 反向代理网页首尾出现神秘字
[52] 解决 nginx 反向代理网页首尾出现神秘字 -
 [46] web开发设计人员不可不用的在线web工具和
[46] web开发设计人员不可不用的在线web工具和 -
 [35] 手机产品设计方向
[35] 手机产品设计方向 -
 [35] 一句话crontab实现防ssh暴力破解
[35] 一句话crontab实现防ssh暴力破解 -
 [33] Rax 系列教程(长列表)
[33] Rax 系列教程(长列表) -
 [28] 程序员疫苗:代码注入
[28] 程序员疫苗:代码注入 -
 [28] 我对学习oracle与成长的理解
[28] 我对学习oracle与成长的理解 -
 [27] 如何建立合适的索引?
[27] 如何建立合适的索引?