首先SVD和LSA是什么呢,SVD全称是singular value decomposition,就是俗称的奇异值分解,SVD的用处有很多,比如可以做PCA(主成分分析),做图形压缩,做LSA,那LSA是什么呢,LSA全称Latent semantic analysis,中文的意思是隐含语义分析,LSA算是topic model的一种,对于LSA的直观认识就是文章里有词语,而词语是由不同的主题生成的,比如一篇文章包含词语计算机,另一篇文章包含词语电脑,在一般的向量空间来看,这两篇文章不相关,但是在LSA看来,这两个词属于同一个主题,所以两篇文章也是相关的。
特征值特征向量
要谈到SVD,特征值和特征向量是需要首先交代的。具体内容可以在wiki上看,这里我做个简单的介绍。对于方阵M如果有
M∗v=λ∗v
v是个向量,
M=Q∗Λ∗Q−1
其中Q是特征向量组成的矩阵,
从另一个角度说如果我们取特征值比较大的几项,那么就是对原矩阵做了一种近似。
M≈Q1..k∗Λ1..k∗Q−11..k
这样我们就可以用更少的元素去近似的表示原矩阵,但是特征分解的限制比较多,比如要求矩阵必须是方阵
奇异值分解
wiki是个好东西,你要想深入了解的话,建议还是去看wiki。奇异值分解是将矩阵变成了这样的形式
M=U∗Σ∗VT
其中
我们还是先回到矩阵是线性变换这个思路上。
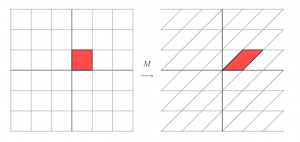
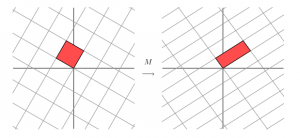
如果我们用M去作用空间里的一组基,那么我们就会得到另一组基,如上图那样。那么我们旋转一下最初的一组基。
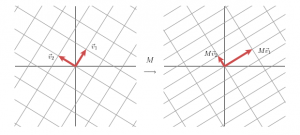
这样我们经过M的变换由一组正交基变换到了另一组正交基上面。也是也就是下面这样。
也就是我们有
M∗v1=σ1∗u1 M∗v2=σ2∗u2
并且对于任意一个向量x,我们有
x=v1∗(vT1∗x)+v2∗(vT2∗x)
于是我们可以得到
M∗x=M∗v1∗(vT1∗x)+M∗v2∗(

 [783]
[783]