五种常用基数估计算法效果实验及实践建议
之前我曾写过一系列关于基数估计(cardinality estimation)算法的文章,文中介绍了一些常用基数估计算法的原理。最近对常用的基数估计算法做了一些实验,这篇文章描述了实验结果,包括这些算法的估计效果及误差状况,主要通过图表展示。通过观察实验数据和可视化图表可以加强对各种基数估计算法理论分析的直观理解。
文章首先会对实验做一些说明,然后通过图表详细展示实验数据,最后会根据实验结果总结一些实践中有用的结论。
实验说明
算法选择
这次实验共选择了五种基数估计算法,分别是:
算法实现使用我所在部门(阿里巴巴商家数据部)的开源基数估计算法库ccard-lib。
数据准备
哈希函数采用murmurhash32(HyperLogLog++采用murmurhash64)。
因实验结果的可靠性仅与哈希值的分布均匀性有关,而根据之前相关研究murmurhash对于顺序型数据具有良好的均匀性。因此为了简化实验,原始数据使用1-1,000,000无符号64bit整型的小端序表示。
下面将通过实验验证原始数据哈希后的均匀性。
实验过程
将原始数据经过murmurhash处理后,验证分桶数在
210 ,212 和216 下数据的均匀性,即看各个桶的元素数量是否大致相等;同时验证各个桶中元素二进制表示的最长0前缀是否服从幂率分布。对五种基数估计算法,分布记录
210 ,212 和216 三种分桶数量下从1到1,000,000的估计值和相对误差值。取样点为100的整倍数,因此共10,000个采样点。比较在
210 ,212 和216 三种分桶数量下五种基数估计算法的误差走势。
实验
数据均匀性
下面首先验证原始数据经过哈希后基本服从均匀分布,从而满足各种基数估计算法的基本前提条件。下面的结果通过murmurhash32哈希值给出,实际中采用murmurhash64得到了基本一致的结论。
对于32bit哈希值,分桶数为
验证分桶均匀性
下面通过柱状图分别给出
murmurhash32哈希值分布(p=10)
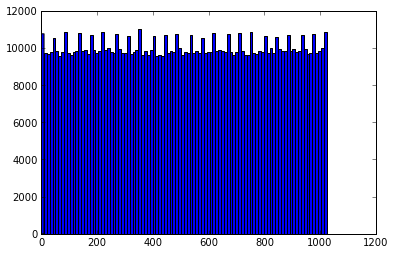
murmurhash32哈希值分布(p=12)
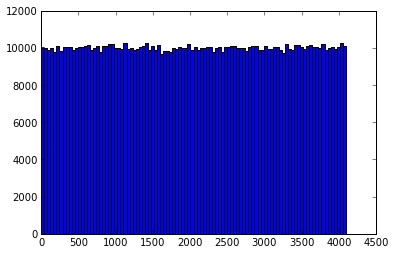
murmurhash32哈希值分布(p=16)
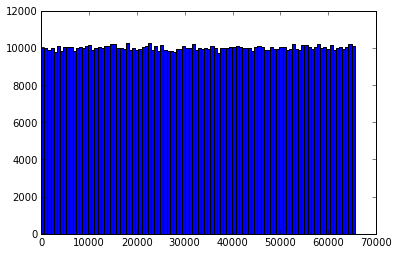
可以看到,三种分桶下数据均基本服从均匀分布。
0后缀长度的幂率分布性
按照理论预言,如果哈希均匀性足够好,哈希剩余部分的关键统计量(最长0后缀长度)应该大约服从底数为2的幂率分布。
下图中横坐标表示0后缀长度,纵坐标表示0后缀为此长度的哈希值个数。
0后缀长度分布(p=10)
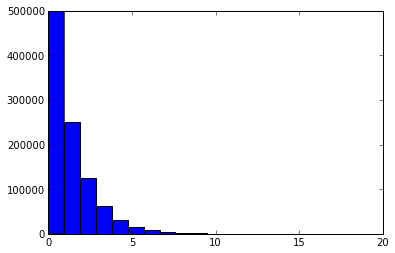
0后缀长度分布(p=12)
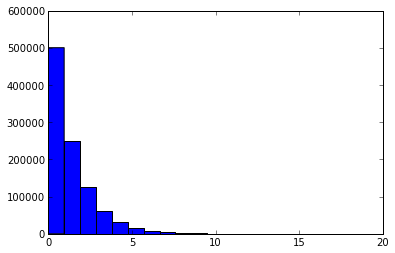
0后缀长度分布(p=16)
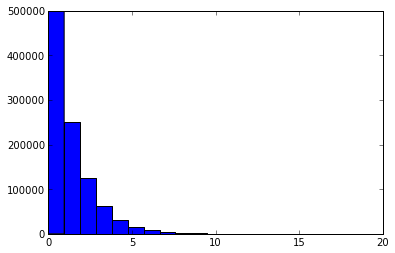
可以看到在三种分桶下统计量分布符合预期。
通过以上分析可知实验数据满足基数估计算法关于均匀性的假设。
基数估计算法效果
下面给出五种基数估计算法的估计效果和误差走势。如未特殊说明,实验分桶数均为
建议继续学习:
- 大数据下的工行 (阅读:6227)
- 企业掘金大数据的两种选择 (阅读:2849)
- 数据化比大数据更靠谱 (阅读:2589)
- 妄谈时间序列表格型大数据系统设计 (阅读:2081)
- 大数据过滤及判断算法 -- Bitmap / Bloomfilter (阅读:1886)
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:ericzhang.buaa@gmail.com 张洋 来源: CodingLabs
- 标签: 估计 基数 大数据
- 发布时间:2013-09-02 13:14:59

 [927]
[927]