两两接触的等粗且无限长的圆柱体
大家在吃饭喝酒时是否注意到了这样的事情:三个人碰杯时,每个人的杯子都能同时和其他两个人的杯子相接触,很完美;但是四个人碰杯时,任一时刻总会有两个人碰不到杯,非常尴尬。有一次和三个好朋友吃饭,四人碰杯时又发生了这种尴尬的情况,突然有一个人异想天开,把他的杯子放到了另外三个杯子的上面,从而实现了四个杯子两两接触!我们自然引出了这样一个问题:如果 n 个全等的圆柱体两两相接触,则 n 最大是多少?
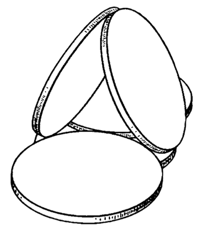
对于不同形状的圆柱体,答案可能是不一样的。 Martin Gardner 在 Hexaflexagons and other mathematical diversions 一书中提到,我们可以精巧地摆放 5 枚硬币,使得它们两两相接触,如上图所示(注意,最底下还藏着一枚硬币)。同时, Martin Gardner 问到,能否摆放 6 支香烟让它们两两接触?一个经典的答案如下:
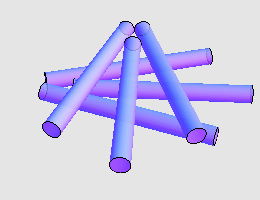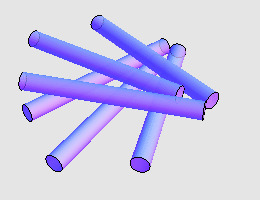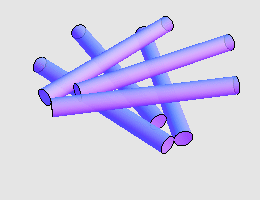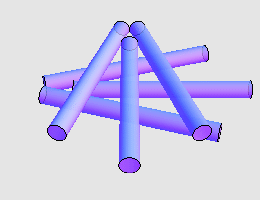
令 Martin Gardner 本人也感到吃惊的是, George Rybicki 和 John Reynolds 指出, 7 支香烟两两接触也是有可能的。他们给出的构造如下:
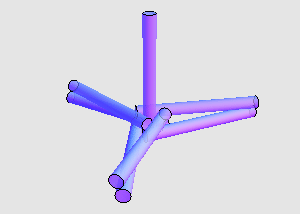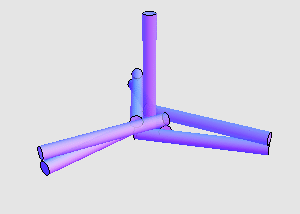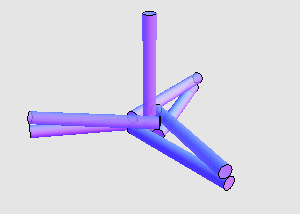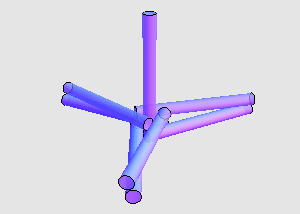
两两接触的全等圆柱体最多可以有多少个? 7 个已经是最多的了吗?如果圆柱体的高度与半径之比有所限制,这会对问题的答案产生怎样的影响?这些问题都还有待解决。
1968 年, John Littlewood 提出了这样一个问题:在空间中,是否存在 7 个单位半径的无限长圆柱体,使得它们两两相接触?这个问题显然更难一些,因为我们没法利用圆柱体的顶面和底面了。
根据 MathPuzzle 的消息,最近, Sándor Bozóki 、 Tsung-Lin Lee 和 Lajos Rónyai 解决了这个问题。他们建立了一个非常非常庞大的方程组,里面有 20 个未知数以及 20 个方程:

通过某些数值计算方法,他们得到了两组不同的解。其中一组解如下:
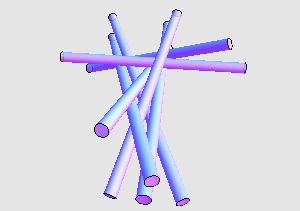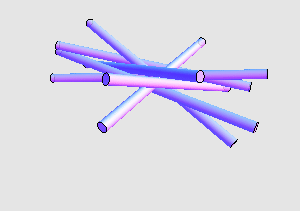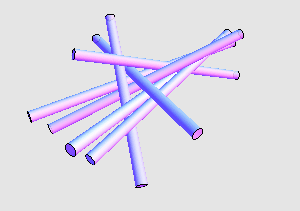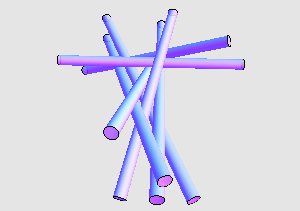
下面则是另外一组解:
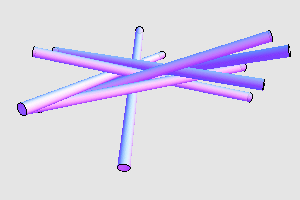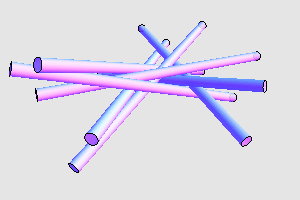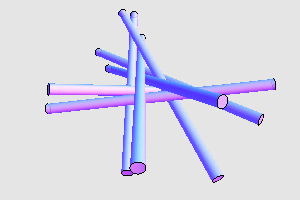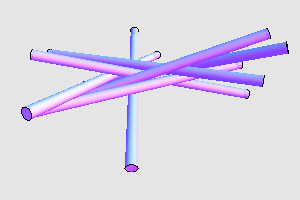
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:Matrix67 来源: Matrix67: My Blog
- 标签: 圆柱体
- 发布时间:2013-11-19 23:18:48
-
 [1167] WordPress插件开发 -- 在插件使用
[1167] WordPress插件开发 -- 在插件使用 -
 [68] 解决 nginx 反向代理网页首尾出现神秘字
[68] 解决 nginx 反向代理网页首尾出现神秘字 -
 [46] Java开发岗位面试题归类汇总
[46] Java开发岗位面试题归类汇总 -
 [44] web开发设计人员不可不用的在线web工具和
[44] web开发设计人员不可不用的在线web工具和 -
 [33] Rax 系列教程(长列表)
[33] Rax 系列教程(长列表) -
 [32] 手机产品设计方向
[32] 手机产品设计方向 -
 [32] 一句话crontab实现防ssh暴力破解
[32] 一句话crontab实现防ssh暴力破解 -
 [29] 程序员疫苗:代码注入
[29] 程序员疫苗:代码注入 -
 [28] oracle技术方面的路线
[28] oracle技术方面的路线 -
 [28] 如何建立合适的索引?
[28] 如何建立合适的索引?