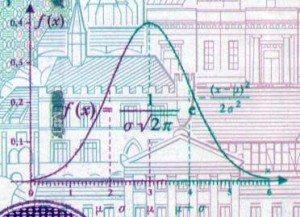
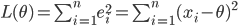您现在的位置:首页 --> 查看专题: 正态分布
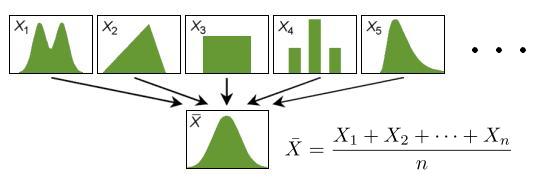
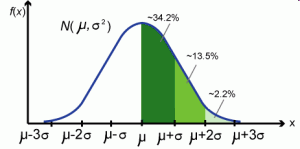
19世纪初,随着拉普拉斯中心极限定理的建立与高斯正态误差理论的问世,正态分布开始崭露头角, 逐步在近代概率论和数理统计学中大放异彩。在概率论中,由于拉普拉斯的推动,中心极限定理发展 成为现代概率论的一块基石。而在数理统计学中,在高斯的大力提倡之下,正态分布开始逐步畅行于天下。
要拉下正态分布的神秘面纱展现她的美丽,需要高深的概率论知识,本人在数学方面知识浅薄,不能胜任。只能在极为有限的范围内尝试掀开她的面纱的一角。棣莫弗和拉普拉斯以抛钢镚的序列求和为出发点,沿着一条小径把我们第一次领到了正态分布的家门口,这条路叫作中心极限定理,而这条路上风景秀丽,许多概率学家都为之倾倒,这条路在20世纪被概率学家们越拓越宽。而后数学家和物理学家们发现:条条曲径通正态。著名的物理学家 E.T.Jaynes 在他的名著《Probability Theory, the Logic of Science》(中文书名翻译为《概率论沉思录》)中,描绘了四条通往正态分布的小径。曲径通幽处,禅房花木深,让我们一起来欣赏一下四条小径上的风景吧。
天文学是第一个被测量误差困扰的学科,从古代至十八世纪天文学一直是应用数学最发达的领域, 到十八世纪,天文学的发展积累了大量的天文学数据需要分析计算,应该如何来处理数据中的观测误差成为一个很棘手的问题。 我们在数据处理中经常使用平均的常识性法则,千百来来的数据使用经验说明算术平均能够消除误差,提高精度。 平均有如此的魅力,道理何在,之前没有人做过理论上的证明。 算术平均的合理性问题在天文学的数据分析工作中被提出来讨论:测量中的随机误差服应该服从怎样的概率分布? 算术平均的优良性和误差的分布有怎样的密切联系?
第二个故事的主角是欧拉(Euler), 拉普拉斯(Lapalace),勒让德Legendre) 和高斯(Gauss),故事发生的时间是十八世纪中到十九世纪初。十七、十八世纪是科学发展的黄金年代,微积分的发展和牛顿万有引力定律的建立,直接的推动了天文学和测地学的迅猛发展。当时的大科学家们都在考虑许多天文学上的问题。
我在大学学习数理统计的时候,学习的过程都是先学习了正态分布,然后才学习中心极限定理。而学习到正态分布的时候,直接就描述了其概率密度的数学形式,虽然数学上很漂亮,但是当时很困惑数学家们是如何凭空就找到这个分布的。然而读了陈希孺的《数理统计学简史》之后,才发现正态分布的密度形式首次发现是在棣莫弗-拉普拉斯的中心极限定理中。数学家研究数学问题的进程很少是按照我们数学课本的安排顺序推进的,现代的数学课本都是按照数学内在的逻辑进行组织编排的,虽然逻辑结构上严谨优美,却把数学问题研究的历史痕迹抹得一干二净,我们难以在数学课本上看到数学家对数学问题是如何研究推进的。DNA 双螺旋结构的发现者之一 Waston 在他的名著《DNA 双螺旋》序言中说:“科学的发现很少会像门外汉所想象的一样,按照直接了当合乎逻辑的方式进行的。”
[ 共5篇文章 ][ 第1页/共1页 ][ 1 ]
近3天十大热文
-
 [1162] WordPress插件开发 -- 在插件使用
[1162] WordPress插件开发 -- 在插件使用 -
 [65] 解决 nginx 反向代理网页首尾出现神秘字
[65] 解决 nginx 反向代理网页首尾出现神秘字 -
 [48] Java开发岗位面试题归类汇总
[48] Java开发岗位面试题归类汇总 -
 [44] web开发设计人员不可不用的在线web工具和
[44] web开发设计人员不可不用的在线web工具和 -
 [33] Rax 系列教程(长列表)
[33] Rax 系列教程(长列表) -
 [32] 一句话crontab实现防ssh暴力破解
[32] 一句话crontab实现防ssh暴力破解 -
 [32] 手机产品设计方向
[32] 手机产品设计方向 -
 [30] 如何建立合适的索引?
[30] 如何建立合适的索引? -
 [29] 程序员疫苗:代码注入
[29] 程序员疫苗:代码注入 -
 [28] oracle技术方面的路线
[28] oracle技术方面的路线
赞助商广告