这是初中平面几何的一个经典问题：等边三角形 ABC 内有任意一点 P，求证 PA 、 PB 、 PC 的长度一定能构成一个三角形。

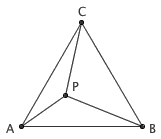
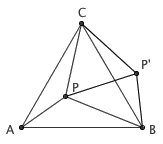
     这里给出两种证明方法。传统的证明方法是，把 △CPA 绕着点 C 逆时针旋转 60 度，从而旋转后的 CA 将会和 CB 重合，同时 P 点落在了 P\' 的位置。由于 △CP\'B 是由 △CPA 旋转过去得到的，因此 P\'B = PA 。另外，线段 CP\' 是 CP 绕着点 C 旋转 60 度得到的，说明 CP 和 CP\' 长度相等且夹角为 60 度，即 △CPP\' 是等边三角形，于是 PP\' = CP 。那么， △BPP\' 的三边长事实上分别等于 PA 、 PB 、 PC ，命题得证。

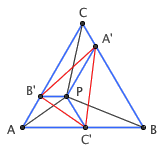
     今天我学到了另外一种证明方法，看上去更简洁巧妙一些。过点 P 分别作三边的平行线，将整个三角形划分为三个蓝色四边形。那么，图中的三个蓝色四边形都有一组对边平行，因而他们都是梯形；事实上，容易看出，这些梯形的两个底角都是 60 度，因而他们都是等腰梯形。只需注意到，等腰梯形的两条对角线长度是相等的，因此红色三角形 A\'B\'C\' 的三边长度事实上就分别等于 PA 、 PB 、 PC ，命题得证。

建议继续学习：

1. 经典证明：任意三角形都能被分成n≥4个等腰三角形    (阅读：4846)
2. 能否在等边三角形点阵中画一个正方形？    (阅读：4178)
3. 三角形变形记之纯css实现的分布导航条效果    (阅读：3514)
4. 出租车几何学：一个全新的几何世界    (阅读：3348)
5. 集数学与艺术于一体的几何幻方    (阅读：2409)
6. 汉字的几何中心    (阅读：2379)
7. 用相同的面组成多面体，凸多面体不一定会更大    (阅读：1811)
8. 网页游戏中的动物世界法则和三角形法则    (阅读：1663)
9. 怎样把一个钝角三角形分成若干个锐角三角形    (阅读：1397)
10. 用CSS绘制各种角度的三角形    (阅读：1137)