有这么两个八面体，它们是由一组相同的三角形面组成的，不过一个是凸多面体，一个是凹多面体。这两个多面体的体积哪个更大？

     不可思议的是，真的就有这么两个八面体，凹的那个比凸的那个更大一些。 2002 年， S. N. Mikhalev 首次发现了这样一对八面体，其中凸多面体的六个顶点分别为

    N(0, 0, 1)，A(10, 1, 0)，B(0, 6, 0)，C(-10, 1, 0)，D(0, -10, 0)，S(0, 0, -1)

     凹多面体的六个顶点则为

    N(0, 0, √61/3)，A(√71, 4√2/3, 0)，B(0, -5√2/3, 0)，C(-√71, 4√2/3, 0)，D(0, -11√2/3, 0)，S(0, 0, -√61/3)

         感兴趣的读者可以自己验证一下，它们的对应棱确实都是一样长的，并且后者的体积确实比前者大。我用 Mathematica 画了一下，两个多面体大致是这样：

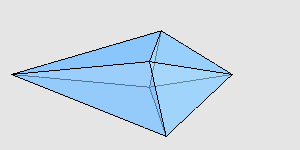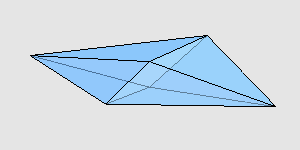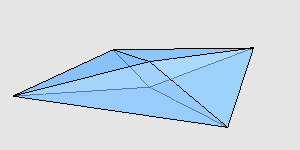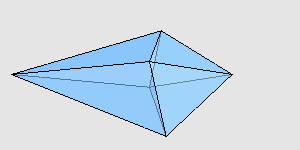
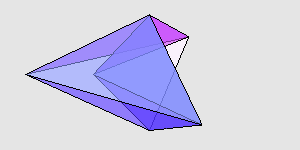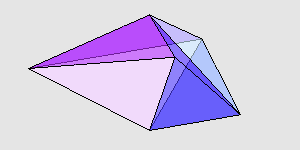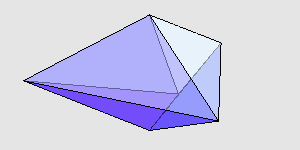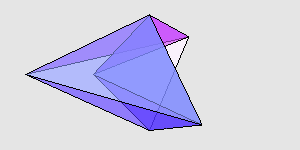
    来源：http://www.cut-the-knot.org/Curriculum/Geometry/Polyhedra/Mikhalev.shtml

建议继续学习：

1. 能否在等边三角形点阵中画一个正方形？    (阅读：4947)
2. 出租车几何学：一个全新的几何世界    (阅读：4242)
3. 经典证明：等边三角形内一点到各顶点的距离长可构成一个三角形    (阅读：3992)
4. 集数学与艺术于一体的几何幻方    (阅读：3203)
5. 汉字的几何中心    (阅读：2946)
6. css3中的几何图形shape研究    (阅读：1853)