这次的趣题来源于 UyHiP 今年八月份的谜题：概率均等地随机选取一个恰好含有 n 个 0 和 n 个 1 的 2n 位 01 串，这个 01 串平均会有多少个 0 和 1 个数相等的前缀(包括空串和整个串本身)？

     为了叙述简便起见，下面我们把所含 0 和 1 个数恰好相等的 01 串叫做平衡的 01 串。例如， 010010110011 就是一个平衡 01 串，它有四个平衡前缀，空串、 01 、01001011 以及整个 01 串本身。我们需要求出的就是，任取一个长为 2n 的平衡 01 串，平衡前缀的个数的期望值是多少。

         注意到，在所有长为 2n 的 01 串中，平衡 01 串一共有 C(2n, n) 个。下面我们证明，所有这些串的所有平衡前缀一共有 4n 个，从而得出问题的答案，即 4n / C(2n, n) 。

     不妨把所有 2n 位平衡 01 串的所有平衡前缀的总数记作 F(n) ，容易得出：

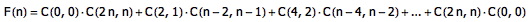
     利用生成函数，我们可以瞬间证明，这个和等于 4n 。由 Taylor 展开可知， 数列 C(2n, n) 所对应的生成函数为：

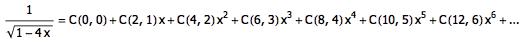
     对上式平方，有：

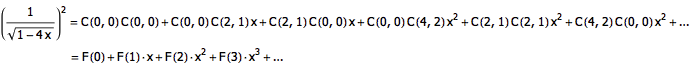
     但

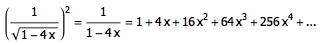
     因此 F(n) = 4n 。

         Joseph DeVincentis 和 Daniel Bitin 给出了一个初等的证明。令 S 为某个平衡 01 串，令 k 为 S 的某个平衡前缀的长度( k 有可能取 0 或者 2n )。我们下面建立一个从所有可能的 (S, k) 到所有长为 2n 的 01 串的一一对应的关系，从而说明所有平衡前缀一共有 4n 个。

     我们先给出把 (S, k) 变换为一个普通 01 串的方法。首先，取 S\' = S 。接下来，找出 S\' 中比 k 更长的平衡前缀中最短的那一个，把它的长度记作 l 。然后，对 S\' 中从第 k + 2 位到第 l 位的数字全部取反。继续寻找新的 l 并执行相应的取反操作，直到 S\' 中不再有比 k 更长的平衡前缀。

     下面我们来说明，这个过程不会无限继续下去，总会有终止的时候。不妨假设 S 的第 k + 1 位是一个 0 。由于取反操作不影响前面 k + 1 位数字，因此 S\' 的前 k 位始终平衡，第 k + 1 位也始终是 0 。容易看出，每次取反前，第 k + 2 位到第 l 位中 1 的个数比 0 的个数多一个，因此对这一段数字取反将会让整个串少一个 1 多一个 0，从而让整个串的后半部分越来越不平衡。因此，总有一个时候，第 k 位以后将会不再有别的平衡点产生。如果 S 的第 k + 1 位是 1 ，类似的推理同样成立。

     然后，我们需要说明，这个对应关系确实是一一对应的。为此，我们需要给出把 S\' 变回 (S, k) 的方法。首先，我们可以很快还原出 k 的值来：找出 S\' 中最长的平衡前缀，它的长度就是 k 。注意， k 一定是偶数，并且有可能是 0 或者 2n 。如果 k 是 2n ，即 S\' 本身就是一个平衡串，那么我们可以直接还原出 S = S\' 。下面只考虑 k < 2n 的情况。

建议继续学习：

1. 打工仔，天下不是我们的    (阅读：5541)
2. UyHiP趣题：限制最苛刻的选票统计程序    (阅读：2030)
3. 控制和开放的平衡，公司内部IT管理的思考    (阅读：1741)
4. UyHiP趣题：拉灯游戏总有解吗？    (阅读：1717)
5. UyHiP趣题：如果每个人都随大流，结果会怎样？    (阅读：1589)
6. UyHiP趣题：按照盒子的三边长之和来计费有没有漏洞？    (阅读：1598)
7. 交互设计实用指南系列(8)―深广度平衡    (阅读：1334)