趣题:把矩形分割为面积相同但形状各不相同的小矩形
Using your Head is Permitted 数学谜题站的主持人 Michael Brand 某日收到了来自 R. Nandakumar 的一个谜题:是否有可能把一个矩形剖分成若干个小矩形,使得每个小矩形的形状互不相同,但它们的面积都一样?没有想到,从这个问题出发,加上一些非常机智巧妙的分析与构造,我们能得到越来越多有意思的东西。于是,它就变成了 Using your Head is Permitted 今年 3 月的谜题。看了谜题的答案后,我也被彻底折服,决定把这一系列的思考重述在此,和大家一同分享。为了简便起见,下面的“矩形剖分方案”一律指的是把一个大矩形分割成若干个小矩形的方案。
让我们先来看一个无关的问题。如果一个矩形剖分方案中不含“子矩形”,我们就说这是一个基本的矩形剖分方案。一个基本的矩形剖分中可能含有多少个小矩形?最平凡的当然是含有 2 个小矩形的基本矩形剖分,最典型的则是含有 5 个小矩形的基本矩形剖分。

对后者继续扩展,我们还能得到含有 7 个小矩形、 8 个小矩形的基本矩形剖分。事实上,对于所有 n = 2 、 n = 5 和 n ≥ 7 的情况,恰好含有 n 个小矩形的基本矩形剖分都是存在的,它们都可以看作是把小矩形螺旋状一圈一圈向外摆放得到的结果。我们下面证明,含有其他数量的小矩形不可能成为基本的矩形剖分方案。这个结论可以用繁冗的分类讨论甚至是计算机程序枚举来完成。我们尽可能用简单巧妙的方法,让证明变得更加可读一些。不感兴趣的读者可以跳过。
考虑某个矩形剖分方案中所有的水平线段。我们把整个大矩形最下面和最上面的两条边叫做边界线段,把其余的水平线段叫做内部线段,并计算这些内部线段一共有多少个不同的纵坐标,把不同纵坐标的个数记作 m 。注意到,如果小矩形的个数 n > 2 ,那么一条边界线段绝不可能被某个小矩形完全霸占(否则会产生子矩形)。每条边界线段一定都被分给了至少两个小矩形。另外,每条内部线段一定都共享给了三个小矩形。如果某条内部线段只被一上一下两个小矩形所用,这两个小矩形就已经构成了子矩形。
于是我们得到,所有小矩形累计有至少 4 + 3m 条水平边。由于每个小矩形有两条水平边,因此小矩形的个数应该满足 n ≥ (4 + 3 m) / 2 。
如果 m ≥ 3 ,则 n ≥ 7 ;如果 m = 2 ,则 n ≥ 5 。另外, m 是不可能等于 1 的,如果矩形剖分里所有的内部线段都在同一个水平位置,那么或者这是一整条从左至右拦腰截断大矩形的线段,从而导致子矩形的出现;或者是一条没能连通左右边界,在中间断开过的线段,这意味着存在一个从上到下贯通整个大矩形的小矩形,同样会导致子矩形的出现。
为了完成我们的证明,我们只剩下 m = 2 并且 n = 6 的情况有待讨论。对竖直边应用相同的推理,可知在此情况下,竖直边也只能有两种不同的横坐标。换句话说,整个矩形剖分只分三层,只有三列,以下面这个 3 × 3 正方形为“模子”。

我们需要把这 9 个格子划作 6 个小矩形,因而至少 3 个小矩形只占一个格子。不妨把这种只占一个格子的小矩形叫做孤立矩形吧。首先,各边中间的格子(即 B 、 D 、 F 、 H)都不能成为孤立矩形。比如,如果 B 是孤立矩形的话,那么 A 、 D 不得不合成一个小矩形, C 、 F 也不得不合成一个小矩形,于是 B 和 E 或者 E 所在的小矩形就构成了子矩形。其次,同侧两个角上的格子也不能同时成为孤立矩形。如果 A 和 C 是孤立的,那么 B 必须和 E 组合起来,从而 A 和包含了 D 的小矩形将构成子矩形。最后,孤立矩形也不能是 A 、 E 、 I 或者 C 、 E 、 G ,否则剩下的形状至少也要被划成 4 个小矩形,总的小矩形个数会超过 6 个。这下,我们便排除了所有的情况。
因此,当且仅当 n = 2, 5, 7, 8, 9, … 时,才存在包含 n 个小矩形的基本矩形剖分。
我们准备好回答本文开头提出的问题了:是否有可能把一个矩形剖分成若干个小矩形,使得每个小矩形的形状互不相同,但它们的面积都一样?自然地,我们更希望找到最简单的、所含小矩形最少的剖分。首先注意到,如果满足条件的矩形剖分包含有子矩形,则这个子矩形同样满足条件。因此,小矩形个数最少的剖分方案必须得是基本的。因此, n 为 3 、 4 、 6 的情况都不用再考虑了。显然,把一个矩形分成面积相等的两个小矩形,它们必然全等,因此 n =2 也就不用考虑了。我们下面要考虑的是 n = 5 的情况。
注意到 n = 5 的基本剖分只能发生在 m = 2 的情况下,因而它仍然是以上图中的九宫格为模子的。据此容易验证,如果把镜像也考虑进来的话,本质不同的剖分就只有一种,就是本文最开头给出的那个图(这里就不再证明了)。为了找出一个所有小矩形面积都相等的剖分,我们假设中间那个小矩形的高为 1 ,宽为 x ,从而小矩形的面积也都得是 x 了。再假设紧邻其右的小矩形宽为 y ,于是所有小矩形的宽和高都能顺次表示出来了:
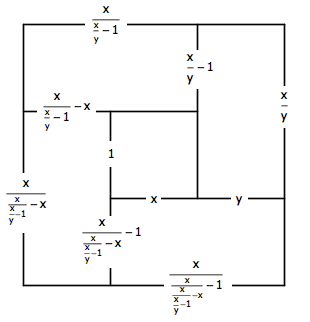
可惜的是,求解 x 和 y 的关系,却发现这个方程没有正数解:
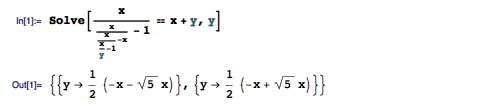
对 n = 7 的情况可以做出类似的分析:
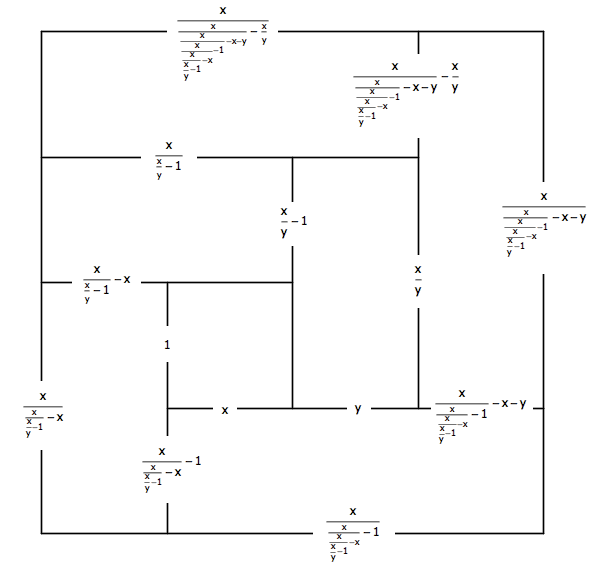
不过这一次,方程有解了:
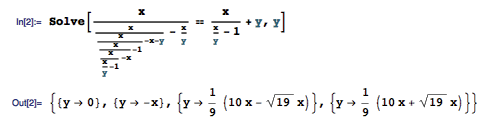
Using your Head is Permitted 给出的解答精心选择了 1 、 x 和 y 的值,使得整个大矩形恰好是一个单位正方形,并且此时所有小矩形正好都互不全等,如下图所示:
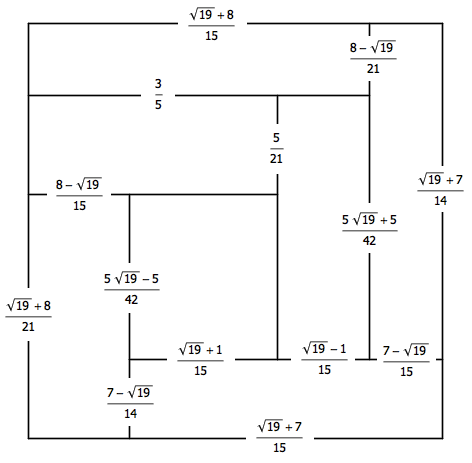
其实这个图历史上已经有人研究过了。它叫做 Blanche\'s Dissection ,可以参见这里。
我们最后的问题就是,对于哪些其他的 n ,小矩形面积都相同但形状互不相同的剖分仍然存在呢?答案是,对于其他所有大于 7 的 n ,满足要求的剖分都是存在的。当 n = 8 时,只需要在上图的最顶部摞一个占满整个宽度并且面积相同的小矩形。当 n = 9 时,则在 n = 8 的构造解的左边加一个占满整个高度并且面积相同的小矩形,以此类推。每一个新加上去的小矩形,其宽度(或者高度)都超过了之前的所有小矩形,因此不会直接与之前的小矩形全等。但是,万一这个新小矩形的宽度恰好等于之前某个小矩形的高度呢?由于所有小矩形的面积都相等,这就意味着前者的高度也将正好等于后者的宽度,这也会导致两个小矩形全等。会不会出现这样的情况还真不敢肯定,不过即使出现了这样的情况,我们也有一个非常巧妙的方法来挽救局面。我们可以对整个矩形进行任意的拉伸(甚至改变原来的长宽比),所有小矩形的面积仍然是相同的。保持整个矩形的高度不变,调整整个矩形的宽度,使得每个小矩形的宽度都不等于任意一个小矩形的高度(比如说,直接把矩形拉到足够宽,使得最小的宽都比整个大矩形的高度更长)。这样一来,所有大于等于 7 的 n 都有了构造解。
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:Matrix67 来源: Matrix67: My Blog
- 标签: 矩形
- 发布时间:2012-05-28 12:17:48
-
 [882] WordPress插件开发 -- 在插件使用
[882] WordPress插件开发 -- 在插件使用 -
 [136] 解决 nginx 反向代理网页首尾出现神秘字
[136] 解决 nginx 反向代理网页首尾出现神秘字 -
 [57] 整理了一份招PHP高级工程师的面试题
[57] 整理了一份招PHP高级工程师的面试题 -
 [55] 用 Jquery 模拟 select
[55] 用 Jquery 模拟 select -
 [54] Innodb分表太多或者表分区太多,会导致内
[54] Innodb分表太多或者表分区太多,会导致内 -
 [54] 分享一个JQUERY颜色选择插件
[54] 分享一个JQUERY颜色选择插件 -
 [54] 如何保证一个程序在单台服务器上只有唯一实例(
[54] 如何保证一个程序在单台服务器上只有唯一实例( -
 [52] CloudSMS:免费匿名的云短信
[52] CloudSMS:免费匿名的云短信 -
 [52] jQuery性能优化指南
[52] jQuery性能优化指南 -
 [51] 海量小文件存储
[51] 海量小文件存储