这是 2008 年莫斯科数学竞赛中的一个问题。构造一个多边形，使得这个多边形的边界上存在这样的一个点 O ：经过点 O 的任意直线均会把该多边形分成面积相等的两份。这看起来不大可能对吧？但其实构造却并不困难。你能想出来吗？

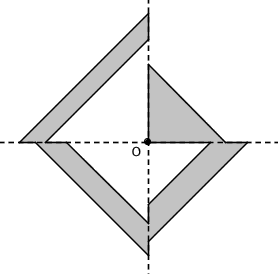
     首先，在平面直角坐标系的第一象限内，沿着坐标轴放置一个等腰直角三角形。在第二象限内，拼接一个面积相等的等腰梯形。在第三象限和第四象限内，继续摆放面积相等的等腰梯形，并且让它们离原点越来越远，以保证最终所得的图形确实是一个多边形(而不是一块环形区域)。现在，把平面直角坐标系的原点记作点 O ，则过点 O 的任意一条直线都将把整个多边形分成面积相等的两份。

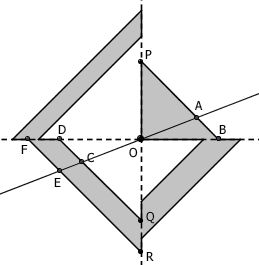
     为了验证这一点，我们举一个例子。如上图，过点 O 作一条过一三象限的直线。容易看出，三角形 OAB 的面积占了三角形 OPB 面积的几分之几，三角形 OCD 的面积就占了三角形 OQD 面积的几分之几，同样地三角形 OEF 的面积就占了三角形 ORF 面积的几分之几，从而梯形 CDFE 的面积就是梯形 QDFR 的几分之几。由于三角形 OPB 的面积等于梯形 QDFR 的面积，因此三角形 OAB 的面积也就总是等于梯形 CDFE 的面积。自然，三角形 OAP 的面积也等于梯形 QCER 的面积了。而第二象限和第四象限的图形面积也是相等的，因此这条直线两侧的面积相等。过点 O 作其他方向上的直线，两侧的面积也相等，道理也一样。

建议继续学习：

1. 正多边形的滚动与旋轮线下方的面积    (阅读：3172)