您现在的位置:首页
--> 算法
• 查找第K小的元素
感觉这是个经典问题了,但是今天看维基百科的时候还是有了新的发现,话说这个问题,比较挫的解决方案有先排序,然后找到第K小的,复杂度是O(nlogn),还有就是利用选择排序或者是堆排序来搞,选择排序是O(kn),堆排序是O(nlogk),比较好的解决方案是利用类似快速排序的思想来找到第K小,复杂度为O(n),但是最坏情况可能达到O(n^2),不过今天要说的,就是还有种方法可以使得最坏情况也是O(n)。
先简单说一下公钥密钥的非对称算法的概念,平常我们用的加密算法往往都是对称的,也就是说加密密钥和解密密钥是一样的,比如凯撒密码,你把每个字母后移3位,a变成d,b变成e,这里3就是加密密钥,然后解密的时候前移3位,这时候3就是解密密钥,非对称加密顾名思义就是加密密钥和解密密钥是不同的,恩,数学就是能干很多神奇的事情啊。
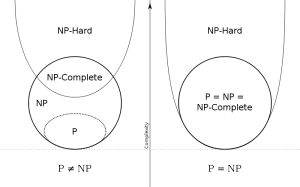
• P和NP那些事
几日前在微博上和清华一博士讨论起一道数据结构选择题,我非常信心满满地给出了答案并且以为是对的,却发现和他给的标准答案相去甚远,去wiki和NIST网站查了一下才知道,原来中国大陆教材中的定义和美国以及我国港澳台地区是完全不同的.本科时用的数据结构教材虽然也是国外的,但是由于当时学习没有注意这些概念,之后就受考研时国内教材和考试的荼毒太深了.
但凡稍微有点资历的程序员,都免不了要写正则表达验证算法。
最近见到好几个正则表达式的Bug,抽空写出来。
拿邮箱验证来说,网上绝大部分人写的邮箱验证正则表达式代码都不能验证这邮箱:
i@julying.com,也不能验证 xxxxxx@i.com 。
首先SVD和LSA是什么呢,SVD全称是singular value decomposition,就是俗称的奇异值分解,SVD的用处有很多,比如可以做PCA(主成分分析),做图形压缩,做LSA,那LSA是什么呢,LSA全称Latent semantic analysis,中文的意思是隐含语义分析,LSA算是topic model的一种,对于LSA的直观认识就是文章里有词语,而词语是由不同的主题生成的,比如一篇文章包含词语计算机,另一篇文章包含词语电脑,在一般的向量空间来看,这两篇文章不相关,但是在LSA看来,这两个词属于同一个主题,所以两篇文章也是相关的。
目录:1. 优雅地使用链表;2. 高效地分支判断;3. 汇编实现的原子操作;4. 0长度数组;5. 三目运算的另类表达
简单来说基于物品的协同过滤算法是说我会推荐给你和你喜欢物品相似的物品,而基于用户的协同过滤算法是说我把和你相似的用户喜欢的东西推荐给你。为什么叫协同过滤呢,因为我们是利用用户的群体行为来作这些相似操作的。计算物品的相似的时候我们比较不同的人来对他打分来比较,同样计算用户相关性的时候我们就是通过对比他们对相同物品打分的相关度来计算的。
Java中的一个byte,其范围是-128~127的,而Integer.toHexString的参数本来是int,如果不进行&0xff,那么当一个byte会转换成int时,对于负数,会做位扩展,举例来说,一个byte的-1(即0xff),会被转换成int的-1(即0xffffffff),那么转化出的结果就不是我们想要的了。
而0xff默认是整形,所以,一个byte跟0xff相与会先将那个byte转化成整形运算,这样,结果中的高的24个比特就总会被清0,于是结果总是我们想要的。
原码表示法是机器数的一种简单的表示法。其符号位用0表示正号,用1表示负号,数值一般用二进制形式表示。设有一数为x,则原码表示可记作[x]原。
数论,数学中的皇冠,最纯粹的数学。早在古希腊时代,人们就开始痴迷地研究数字,沉浸于这个几乎没有任何实用价值的思维游戏中。直到计算机诞生之后,几千年来的数论研究成果突然有了实际的应用,这个过程可以说是最为激动人心的数学话题之一。
寄存器分配是编译器中一个历久弥新的问题,因为它是编译器在输出汇编代码前必须经历的阶段。寄存器分配算法的好坏,关系着生成代码的性能,大小。为了追求极致性能,很多编译器都在寄存器分配上做了很多文章,不惜引入非常复杂的算法。另一方面寄存器分配算法本身的性能也很关键, 在诸多的JIT编译器(Just-In-Time compiler)中,编译器的性能同时也是程序本身的性能,因此在JIT编译器中还需要关注寄存器分配算法本身的效率问题。
主要对一般docId为下标对应域值的结构做了改造,如果大家有更好的建议,欢迎大家提议和拍砖。 主要思路: 生成一个下标为 域 Term 遍历的Postion 且值为域值的数组: A[p]=field value 因为域值并不会像docId一样为唯一键递增,所以在创建的时候 初始化: Int [] A = new Int[reader.maxDoc()] 结束的时候如果 p
• 基数估计算法概览
基数估计算法使用很少的资源给出数据集基数的一个良好估计,一般只要使用少于1k的空间存储状态。这个方法和数据本身的特征无关,而且可以高效的进行分布式并行计算。估计结果可以用于很多方面,例如流量监控(多少不同IP访问过一个服务器)以及数据库查询优化(例如我们是否需要排序和合并,或者是否需要构建哈希表)。
要拉下正态分布的神秘面纱展现她的美丽,需要高深的概率论知识,本人在数学方面知识浅薄,不能胜任。只能在极为有限的范围内尝试掀开她的面纱的一角。棣莫弗和拉普拉斯以抛钢镚的序列求和为出发点,沿着一条小径把我们第一次领到了正态分布的家门口,这条路叫作中心极限定理,而这条路上风景秀丽,许多概率学家都为之倾倒,这条路在20世纪被概率学家们越拓越宽。而后数学家和物理学家们发现:条条曲径通正态。著名的物理学家 E.T.Jaynes 在他的名著《Probability Theory, the Logic of Science》(中文书名翻译为《概率论沉思录》)中,描绘了四条通往正态分布的小径。曲径通幽处,禅房花木深,让我们一起来欣赏一下四条小径上的风景吧。
MinHash首先它是一种基于 Jaccard Index 相似度的算法,也是一种LSH的降维的方法,应用于大数据集的相似度检索、推荐系统。下边按我的理解介绍下MinHash。 举例A,B 两个集合: A = {s1, s3, s6, s8, s9} B = {s3, s4, s7, s8, s10} 根据Jaccard Index公式,A,B的相似度 S(A,B) = |A∩B|/|A∪B| = 2/8 = 0.25, 用图表示如下: 当然直接计算两个集合的交集与并集,是很耗计算资源的,特别是在海量数据场景下不可行。 假如,我们随机从两个集合中各挑选一个元素s(A)、s(B),刚好这两个无素相同的概率是多少呢?
最近一个项目在使用JsonCpp,JsonCpp简洁易用的接口让人印象深刻。但是在实际使用过程中,我发现JsonCpp的性能却不尽如人意,所以想着方法优化下性能。
最近的工作让我想到了一个对集合的元素进行并行聚合的案例,尽管这个需求还不存在,但最近却一直在我的脑海里挥之不去,尚未得出令人满意的结果。今天下班前我将这个问题辛苦地缩减为140字内的描述发到了微博上,得到了许多同学的回复,但可能是由于描述过于简单,得到的建议似乎都不能满足我的需求。于是在此我通过博客详细描述下这个问题的需求,还有我之前做过的尝试,这样讨论起来也可以更加有针对性一些。
近3天十大热文
-
 [1086] WordPress插件开发 -- 在插件使用
[1086] WordPress插件开发 -- 在插件使用 -
 [76] Java开发岗位面试题归类汇总
[76] Java开发岗位面试题归类汇总 -
 [47] web开发设计人员不可不用的在线web工具和
[47] web开发设计人员不可不用的在线web工具和 -
 [41] 一句话crontab实现防ssh暴力破解
[41] 一句话crontab实现防ssh暴力破解 -
 [37] Rax 系列教程(长列表)
[37] Rax 系列教程(长列表) -
 [33] 手机产品设计方向
[33] 手机产品设计方向 -
 [32] 解读iPhone平台的一些优秀设计思路
[32] 解读iPhone平台的一些优秀设计思路 -
 [31] cookie窃取和session劫持
[31] cookie窃取和session劫持 -
 [31] 程序员疫苗:代码注入
[31] 程序员疫苗:代码注入 -
 [31] 基于综合兴趣度的协同过滤推荐算法
[31] 基于综合兴趣度的协同过滤推荐算法
赞助商广告