趣题:证明所有乘积的总和与分拆的方式无关
有 1000 枚硬币堆在一起。把它们任意分成两堆,并计算出这两堆的硬币数的乘积。然后,任意选择其中的一堆硬币,把它继续分成两个更小的堆,并计算出这两堆的硬币数的乘积。不断这样做下去,直到最后每堆都只剩一枚硬币为止。求证:把途中产生的所有乘积全部加在一起,结果是一个定值,它不随分法的改变而改变。
这是一个非常经典的问题。让我们把 1000 枚硬币换成 n 枚硬币,这样的话问题反而会更容易一些。如果初始时有 n 枚硬币,把它们分到底后,产生的所有乘积之和是多少呢?考虑一种特殊的分法:把 n 分成 1 和 n - 1 两堆,再把 n - 1 分成 1 和 n - 2 两堆……显然,由此得到的总和应该是 (n - 1) + (n - 2) + ... + 2 + 1 = n(n - 1) / 2 。有了这个公式后,我们便很容易用数学归纳法证明,不管分法是什么,最终的结果一定是 n(n - 1) / 2 。首先验证,当 n = 1 时, n(n - 1) / 2 = 0 ,这是符合实际情况的:单独一枚硬币不会产生任何新的乘积。对于一般的 n ,把它分成 x 和 n - x 两堆,得到乘积 x(n - x) 。由归纳假设,这两堆硬币今后将各产生总和为 x(x - 1) / 2 的乘积,以及总和为 (n - x)(n - x - 1) / 2 的乘积。不难算出,x(n - x) + x(x - 1) / 2 + (n - x)(n - x - 1) / 2 正是 n(n - 1) / 2 。
其实,这个问题有一个异常帅的秒杀方法。每次把一堆硬币分成两堆后,计算两堆硬币数量的乘积,实际上相当于是在计算有多少对硬币在这一步被分开了。最后所有乘积的总和,也就是在整个过程中被分开的硬币对的总数。然而, n 枚硬币之间共有 C(n, 2) = n(n - 1) / 2 个硬币对,所有的硬币对最终都被分开了,因而问题的答案就是 n(n - 1) / 2 ,这不随分法的变化而变化。
现在,让我们把问题变一下。假设有一根长度为 n 的线段。把它分成两条子线段,并计算这两条子线段的长度的乘积。选择其中一条子线段,并把它继续分成两条更小的子线段,求出这两条子线段的长度的乘积。不断这样细分下去,直到所有的子线段长度都趋于 0 。在此过程中,不断累加所得的乘积,其总和的极限是多少?(注意,这里的描述还需要更严谨一些,不过我们暂不追究。)
显然,答案应该是一个比 n(n - 1) / 2 更大的数。因为根据前一个问题的解答,把长度为 n 的线段分成 n 个长度为 1 的线段,乘积的总和为 n(n - 1) / 2 ;但在此之后,我们还可以继续切分线段,让总和继续增加。那么,答案究竟是多少呢?我们也可以借助某个特殊的分法得出答案。假设我们按照如下方法把线段无穷细分:先把整条线段等分成两段,得到乘积 (n / 2)2 ;再把所得的两条子线段都进行平分,得到两个 (n / 4)2 ;再依次平分当前的四条子线段,得到四个 (n / 8)2 ……以此类推,最后的总和将会是 (n / 2)2 + 2 · (n / 4)2 + 4 · (n / 8)2 + 8 · (n / 16)2 + ... = n2 / 4 + n2 / 8 + n2 / 16 + n2 / 32 + ... = n2 / 2 。
不过,我们如何证明,任意一种分法都会导致总和最终会趋于 n2 / 2 ?升级版的问题变得不再离散,数学归纳法和组合方法似乎都派不上用场了。其实,借助几何构造,这个问题也有一个非常直观的秒杀方法。
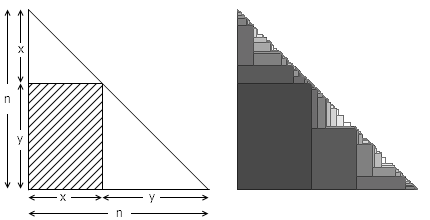
如图,初始时线段的总长为 n ,那么我们就作一个边长为 n 的等腰直角三角形。如果把线段分成了 x 和 y 两段,由此产生的乘积 x · y 就对应于左图的等腰直角三角形中阴影矩形的面积。继续细分两个子线段,也就相当于递归地处理两个剩余的空白三角形。当所有子线段都被分到无穷短时,矩形面积的总和将会无穷接近于整个等腰直角三角形的总面积,也就是 n2 / 2 。
扫一扫订阅我的微信号:IT技术博客大学习
- 作者:Matrix67 来源: Matrix67: My Blog
- 标签: 乘积 分拆
- 发布时间:2012-11-02 13:04:35
-
 [927] WordPress插件开发 -- 在插件使用
[927] WordPress插件开发 -- 在插件使用 -
 [126] 解决 nginx 反向代理网页首尾出现神秘字
[126] 解决 nginx 反向代理网页首尾出现神秘字 -
 [51] 如何保证一个程序在单台服务器上只有唯一实例(
[51] 如何保证一个程序在单台服务器上只有唯一实例( -
 [50] 整理了一份招PHP高级工程师的面试题
[50] 整理了一份招PHP高级工程师的面试题 -
 [48] CloudSMS:免费匿名的云短信
[48] CloudSMS:免费匿名的云短信 -
 [48] Innodb分表太多或者表分区太多,会导致内
[48] Innodb分表太多或者表分区太多,会导致内 -
 [48] 用 Jquery 模拟 select
[48] 用 Jquery 模拟 select -
 [48] 全站换域名时利用nginx和javascri
[48] 全站换域名时利用nginx和javascri -
 [48] 海量小文件存储
[48] 海量小文件存储 -
 [46] ps 命令常见用法
[46] ps 命令常见用法