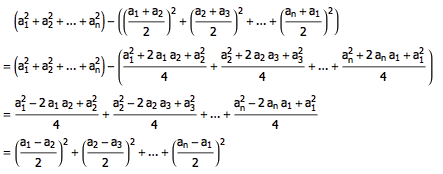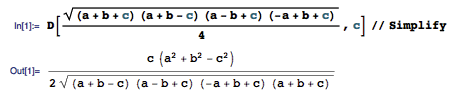您现在的位置：首页
--> 算法
String对我们来说太熟悉了，因为它无处不在，更因为用String可以描述这个世界几乎所有的东西，甚至于为了描述精确的数值都需要String出马（因为计算机眼中的二进制和人类眼中的十进制间总有那么点隔膜）。因为熟悉而变得简单，也容易被忽略。今天记录一下关于String的容易被忽略的两个问题。 字符串重用――节省内存 因为字符串太多，如果能够重用则能够节省很大的内存。首先看下面一个例子： String string1 = “HEL...
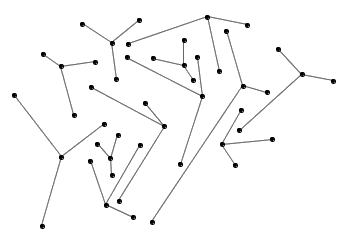
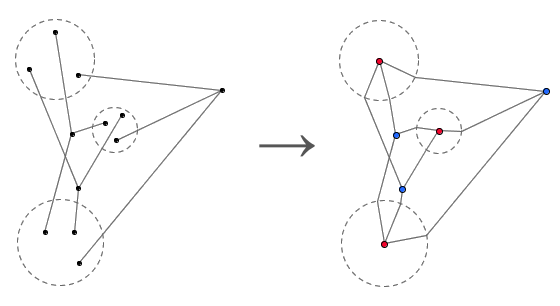
在集合 {1, 2, ..., n} 中选出尽可能多的子集，使得每个子集所含的元素个数都是奇数，但是任意两个子集的交集都含有偶数个元素。那么，我们最多能够选出多少个这样的子集来？ 容易看出，我们至少可以选出 n 个子集。例如，当 n = 4 时， {1} 、 {2} 、 {3} 、 {4} 就满足要求。我们还能选出更多的子集来吗？简单地尝试后，你会觉得似乎不行。不过，这却并不是显然的，因为存在一...
• Scala很难
首先要说的是，我是一个Scala粉丝，我作为一个Scala语言的倡导者差不多有5年历史了。我写了不少Scala语言方面的书和文章。我曾在数十个公司里做过Scala和Lift框架项目的开发。我对很多的Scala项目进行过代码审查。 我过去以为Scala很简单。它过去确实很简单，而且一直很简单，它是治疗Java里很多问题的良方。从“有些使用Java显的异常的困难或不可能的事,使用Scala却非...
这篇文章收录了 Which Way Did the Bicycle Go 趣题集中一个非常有趣的问题：是否有可能在平面上画不可数个不相交的 8 ？答案是否定的。证明方法非常简单。对于任意一个 8 字形，在两个洞里各取一个有理点 P 、 Q （由于平面上的有理点是稠密的，这是总能办到的），则称这个 8 字形圈住了有理点对 (P, Q) 。注意到由于 8 字形不能相交，因此两个 8 字形不可能圈住同一对有理点。由于平面上的有理点对是可...
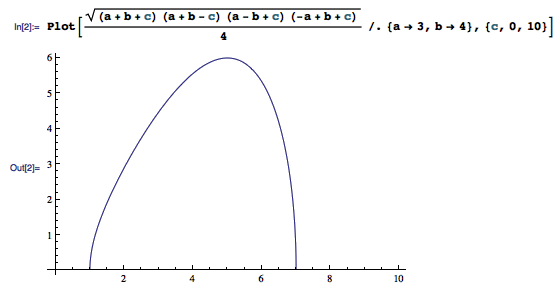
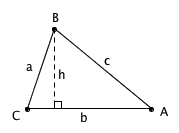
Heron 公式是一个已知三角形三边长便能直接求出其面积的经典公式。把三角形的三边长分别记作 a 、 b 、 c ，令三角形的半周长 p = (a + b + c) / 2 ，则三角形的面积可以用 Heron 公式 S = √p(p - a)(p - b)(p - c) 求出。如果把 p = (a + b + c) / 2 代入式子，得到的公式其实也挺对称的： S = √(a + b + c)(a + b - c)(a - b + c)(- [...]
这是一个关于C\C++程序员的一个小故事，关于C++11――刚刚通过的新标准的一个小故事… 请不要误会，题目中所提及的“优化”并不是提升程序的性能――Lambda表达式干不了这个。从本质上来说，它只是一种“语法糖”而已。不使用这种表达式，我们照样可以写出满足需求的程序。正如放弃C而使用汇编，或者放弃汇编而使用机器语言一样，你能控制的范围就在那里，不增不减。但如果有得选择，我相信大部分人会选择汇编而非机器语言，选择...
• 用抛物线筛选质数
在下面的问题中，你不能使用圆规，只能使用直尺作图。不过，你的直尺拥有两条平行边，你可以在作图时同时使用它们。你需要充分利用直尺的这个特点，完成下面几个作图任务。 1. 作出已知角的角平分线； 2. 作出已知线段的中点； 3. 作出已知圆的圆心； ...
题外话最近计划对Memcached做一些尝试性的改造，主要是针对Memcached在处理过期数据的时候进行改造，以实现在一个缓存的过期时间达到的时候，可以对该缓存的数据进行一个验证和存储的处理。 ...
PHP 5.4 由Arnaud 引入了一个对三元式的优化方案. 我们都知道PHP用写时复制来对变量复制做性能优化, 而在以前的三元式中, 却每次都会复制, 这在操作数是大数组的情况下, 会造成性能问题。
许多快递公司都依据物件的长、宽、高三边之和来收费，一些航空公司也要求托运行李的三边长相加不能超过某个限制。那么是否有人想过，有没有可能把一个三边之和较大的盒子装进一个三边之和较小的盒子里，从而骗取更低的费用呢？有人会说，恐怕不行吧，长宽高之和更大的盒子体积不也应该更大一些吗？不见得。比方说，盒子 A 的长宽高分别是 ...
最近有同学在gmail上问关于gen_tcp发送进程被挂起的问题，问题描述的非常好，见底下： 第一个问题是关于port_command和gen_tcp:send的。从项目上线至今，我在tcp发送的地方遇到过两次问题，都跟port_command有关系。 起初程...
gen_tcp:unrecv是个未公开的函数，作用是往tcp的接收缓冲区里面填入指定的数据。别看这小小的函数，用起来很舒服的。
什么是数据挖掘？ 数据挖掘是商务智能应用中较高层次的一项技术，而商务智能中还包括数据仓库、ETL、联机分析、商业报表等多项技术。数据挖掘在商务智能应用中提供的是一种自动化或半自动化的数据分析手段，利用数据挖掘用户将可以更加方便地发现数据的模式（其实就是用户关心的业务模式），用户还可以利用这些模式对某些符合特征的数据作出预测。 那么数据挖掘究竟是怎么做到上面这些貌似神奇的事情的呢？现在主流的数据挖掘技术...
一个小学奥数老师给我讲了一道小学奥数题，这是他在上课时遇到的：从 1 到 4000 中，各位数字之和能被 4 整除的有多少个？ 注意，问题可能没有你想的那么简单，满足要求的数分布得并没有那么规则。 1 、 2 、 3 、 4 里有一个满足要求的数， 5 、 6 、 7 、 8 里也有一个满足要求的数，但是 9 、 10 、 11 、 12 里就没有了。 尽管如此，这个问题仍然有...
• GFS论文重读
Google文件系统（Google File System，GFS）是构建在廉价的服务器之上的大型分布式系统。它将服务器故障视为正常现象，通过软件的方式自动容错，在保证系统可靠性和可用性的同时，大大减少了系统的成本。 GFS是Google云存储的基石，其它存储系统，如Google Bigtable，Google Megastore，Google Percolator均直接或者间接地构建在GFS之上。另外，Google大规模批处理系统MapReduce也需要利用GFS作为海量数据的输入输出。 系统架构 GF...
这个并不是标题党。很多年以前，要想进入莫斯科国立大学的数学系，你必须通过四项入学考试；头两个都是数学考试，一个笔试，一个面试。在面试中，学生和考官都是一对一的，考官可以自由向学生提出任何他喜欢的问题。考官们都准备了很多“棺材问题”，这些问题的答案非常简单，但由于思路太巧妙了，以至于学生很难想到。考官便可以以“你连这个都没想到”为理由，光明正大地拒绝学校不想要的人（主要是犹太...
以下内容摘自myThoughtWorks中对于结对编程(Pair Programming)的讨论。 结对编程与非结对编程相比那个效率会更高？ 这个问题没有一个明确的答案，没有人可以很肯定的说结对编程就是会比非结对编程更有效率。效率不单单是时间，还包含效果。 如果对于一个技术难度不高，一个人几天就可以搞定，后期不需要维护的一个小项目来说可能结对编程在效率上会低于非结对编程。但是我们twer是关注代码质量 的，面临的项目一般都是需要持续发展...
近3天十大热文
-
[77] WEB系统需要关注的一些点 -
[18] 浏览器的工作原理：新式网络浏览器幕后揭秘
-
[13] Spark性能优化——和shuffle搏斗
-
[13] Android设计中的.9.png
-
[12] 我的git笔记
-
[11] 内网穿透神器frp
-
[10] 深入剖析 redis replication
-
[10] Python程序的执行原理
-
[10] 界面设计速成
-
[10] Python 代码规范小结
赞助商广告
