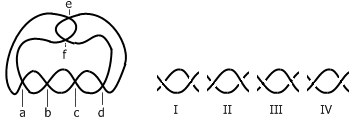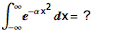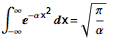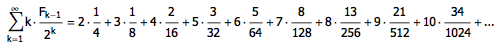您现在的位置：首页
--> 算法
【什么是双层桶】 事实上，与其说双层桶划分是一种数据结构，不如说它是一种算法设计思想。面对一堆大量的数据我们无法处理的时候，我们可以将其分成一个个小的单元，然后根据一定的策略来处理这些小单元，从而达到目的。 【适用范围】 第k大，中位数，不重复或重复的数字 【基本原理及要点】 因为元素范围很大，不能利用直接寻址表，所以通过多次划分，逐步确定范围，然后最后在一个可以接受的范围内进行...
各位C、C++开发的朋友们，有没有想过小小的printf也会有陷阱呢？这篇文章，我们就深入来探究一下（代码均在suse10 32位系统下编译测试通过）。
很早以前，我简单介绍过 Julia 集和 Mandelbrot 集，文章在此。这可以说是数学中最神秘、最令人敬畏的研究对象之一。不过，那时我对这个话题了解还不太深。今天见到这个网页，让我对 Julia 集和 Mandelbrot 集有了更深的了解。我查阅了一些其他的资料，然后写下这篇长文，与大家一同分享。继续阅读以前，建议先看看我原来那篇文章（很短），那里面有很多漂亮的 Julia 集和 Mandelbrot 集的图片，这篇文章...
广大码农同学们大多都有个共识，认为算法是个硬骨头，很难啃，悲剧的是啃完了还未必有用――除了面试的时候。实际工程中一般都是用现成的模块，一般只需了解算法的目的和时空复杂度即可。 不过话说回来，面试的时候面算法，包括面项目中几乎不大可能用到的算法，其实并不能说是毫无道理的。算法往往是对学习和理解能力的一块试金石，难的都能掌握，往往容易的事情不在话下。志于高者得于中。反之则不成立。另一方面，虽说教科书算...
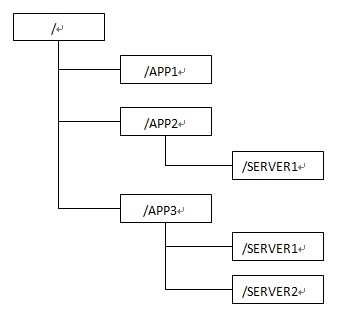
zookeeper介绍 zookeeper是一个为分布式应用提供一致性服务的软件，它是开源的Hadoop项目中的一个子项目，并且根据google发表的论文来实现的，接下来我们首先来安装使用下这个软件，然后再来探索下其中比较重要一致性算法。
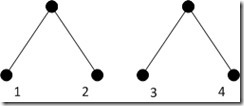
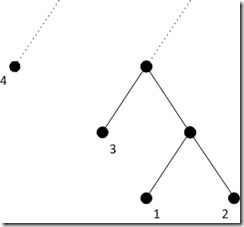
ConcurrentHaspLRUHashMap实现初探 一、 关于LRU。 LRU 即 Least Rencetly Used（最近最少使用）缓存替换策略。在任何LRU算法中，它必定有以下两个策略组成： 1、 退化 策略。根据访问情况，对节点按热度进行排序（hot->cold），以便决定哪些节点是热节点（hot）的，哪些节点是冷节点（cold）的。这个退化的策略，一般按以下两种方式去处理： l 非集中式。即每命中一次就进行退化操作。 非集中式的退化操作，往...
在即将到来的C++1x标准中，一个重大的更新就是引入了C++多线程内存模型。本文的主要目的在于介绍C++多线程内存模型涉及到的一些原理和概念，以帮助大家理解C++多线程内存模型的作用和意义。
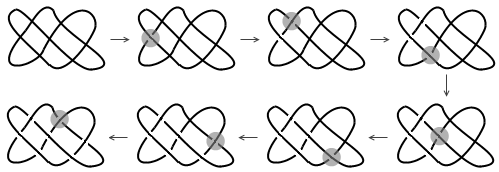
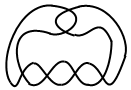
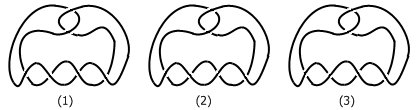
A Midsummer Knot’s Dream 简直可以说是去年学术界的一篇奇文，大家点进去看看就知道了。论文里讲了一个基于纽结理论的双人对弈游戏，名字也非常有艺术感： To Knot or Not to Knot 。这个游戏可能是最难的组合游戏了，它的数学性极强，思考难度非常大，甚至比 ERGO 更不容易上手。一场游戏下来，究竟谁赢谁输可能都不好判断。 To Knot or Not to Knot 的游戏规则非常简单。用铅...
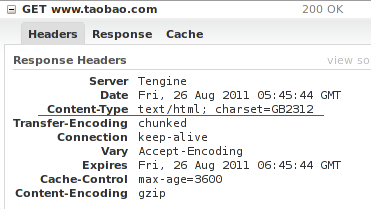
导语：由于历史原因，淘宝网的页面编码一直都是gbk，F2E手册中也有明确规范，刚开始的一段时间，F2E们并未遭遇太麻烦的乱码问题，大家相安无事，但随着淘宝的合作方越来越多，合作方的API接口编码可谓五花八门，淘宝的系统和第三方的数据对接之后就暴露出各式各样的乱码问题。有必要再把这个问题缕缕清楚。 我想，可能是在做第一个淘宝网的页面时，工程师只顾写代码，而忘了看一看编辑器的默认编码设置，再后来就将错就错直到今天...
当 1848 年国际象棋玩家 Max Bezzel 提出八皇后问题（eight queens puzzle）时，他恐怕怎么也想不到，100 多年以后，这个问题竟然成为了编程学习中最重要的必修课之一。八皇后问题听上去非常简单：把八个皇后放在国际象棋棋盘上，使得这八个皇后互相之间不攻击（国际象棋棋盘是一个 8×8 的方阵，皇后则可以朝横竖斜八个方向中的任意一个方向走任意多步）。虽然这个问题一共有 92 个解，但要想徒手找出一...
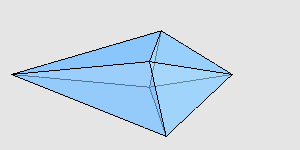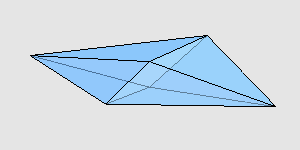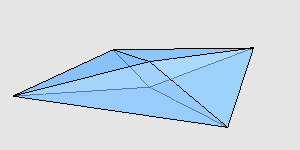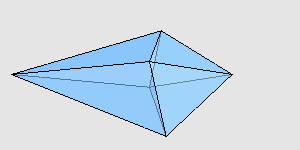
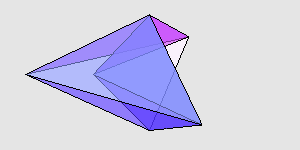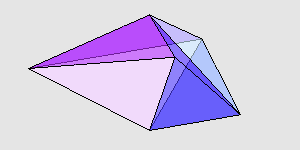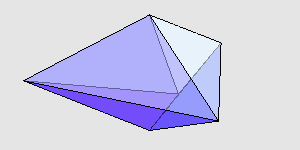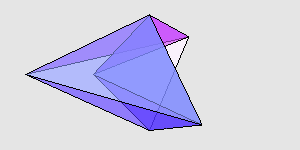
有这么两个八面体，它们是由一组相同的三角形面组成的，不过一个是凸多面体，一个是凹多面体。这两个多面体的体积哪个更大？ 不可思议的是，真的就有这么两个八面体，凹的那个比凸的那个更大一些。
公式 h = (1/2)・g・t^2 里， t 头上的平方并不奇怪。显然，物体下落的路程是与重力加速度 g 和时间 t 有关的，高度 h 就由这两个变量决定。注意到 g 是一个加速度单位，是米除以平方秒的形式；为了得出一个以长度为单位的结果，我们必须要消除分母位置上的“平方秒”，因而时间变量 t 必须要以平方的形式出现。 类似地， E = m・c^2 里的平方也不是凭空而来的。能量的单位是牛乘...
她是一款神奇的小游戏，老少皆宜，百玩不厌，她是给一堆图案中的相同图案进行配对的简单游戏，在2003年，一个叫做朱俊的网友将这种形式搬到了PC上，立刻成为办公一族的新宠，并迅速传遍了世界各地，她就是连连看。没想到这几日我却和它邂逅出了一段趣事，而这一切都源于前几日我所在公司某产品在内部群里的一段对白： 蒋某：大家看这个页面，用户的头像怎么有重复的呢？又不是做连连看啊~ 任某：Hoho，我们反倒不如在这个页面埋个...
今天碰上一个非常有意思的问题。有一条通信线路，每次可以发送一个由数字 0 到 9 组成的任意长的数字串。怎样巧妙地利用这条通信线路，构造一种一次能够发送两个数字串的协议？注意到，直接将两个数字串相连是不行的，因为这将会产生歧义。如果对方收到的数字串是 1234 ，他没法知道你发送的是数字串 12 和 34 ，还是数字串 123 和 4 ，抑或是 1 和 234。 能否把第一个串的位数编...
但凡初次接触MongoDB的人，无不惊讶于它对内存的贪得无厌，至于个中缘由，我先讲讲Linux是如何管理内存的，再说说MongoDB是如何使用内存的，答案自然就清楚了。
今天又学到一种证明素数无穷多的方法。它是由 Filip Saidak 发现的，论文曾发表在 2006 年的 The American Mathematical Monthly 上。 首先注意到，两个相邻自然数一定是互质的（否则，假设他们有大于 1 的公因数 k ，则他们的差也能被 k 整除，这显然是不可能的）。现在，取一个自然数 n > 1 。由于 n 和 n + 1 是相邻自然数，因此 n 和 n + 1 是互质的。也就是说，n 的质因数和...
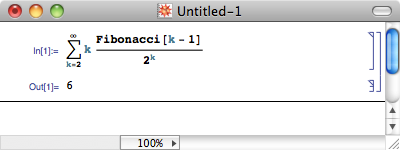
在一篇老日志中，我提到了一个经典的概率问题：平均需要抛掷多少次硬币，才会首次出现连续两个正面？它的答案是 6 次。它的计算方法大致如下。 首先，让我们来考虑这样一个问题： k 枚硬币摆成一排，其中每一枚硬币都可正可反；如果里面没有相邻的正面，则一共有多少种可能的情况？这可以用递推的思想来解决。不妨用 f(k) 来表示摆放 k 枚硬币的方案数。我们可以把这些方案分成两...
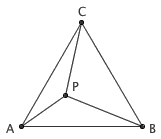
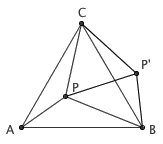
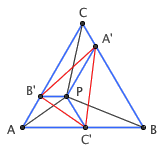
这是初中平面几何的一个经典问题：等边三角形 ABC 内有任意一点 P，求证 PA 、 PB 、 PC 的长度一定能构成一个三角形。 这里给出两种证明方法。传统的证明方法是，把 △CPA 绕着点 C 逆时针旋转 60 度，从而...
近3天十大热文
-
[44] WEB系统需要关注的一些点 -
[18] 浏览器的工作原理：新式网络浏览器幕后揭秘
-
[13] Android设计中的.9.png
-
[12] 我的git笔记
-
[12] 内网穿透神器frp
-
[11] Spark性能优化——和shuffle搏斗
-
[11] 界面设计速成
-
[10] Python程序的执行原理
-
[10] 深入剖析 redis replication
-
[10] Python 代码规范小结
赞助商广告
